本篇文章简单介绍了三种矩阵分解方式并且附上部分分解方式的实现代码。
矩阵分解
Python实现了QR与LU分解,QR用了两种变换方式实现。Github地址
What?
将矩阵拆分成数个三角形矩阵。
Why?
- 数值分析中,用于实现一些矩阵运算的快速算法
- 推荐算法(SVD),信号处理(SVD)
- 反应矩阵中的一些数值特性:如矩阵的秩、特征值(奇异值)
每一种矩阵分解方式对应不同的意义
How?
基本概念介绍
关于转置、逆矩阵就不多介绍了。
- 满秩矩阵
- 矩阵的秩等于行数—>行满秩
- 矩阵的秩等于列数—>列满秩
- 以上两个都满足称为n阶方阵
- 酉矩阵(正交矩阵)
- 方块矩阵,元素皆为实数,行与列皆正交的单位向量
- 特性:矩阵的转置矩阵为逆矩阵
- 定理(det表示行列式):
\[Q^T=Q^{-1}\Leftrightarrow Q^TQ=QQ^T = I\]
\[1=\det(I)=\det(Q^TQ)=\det(Q^T)\det(Q)=(\det(Q))^2\Rightarrow|Q| \pm 1\]
单位矩阵
- 矩阵中的每个元素都为1
- 如下
\[\left| \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1& 1 & 1 \end{array} \right|\]
上三角矩阵
- 非零元素在右上方的矩阵
- 如下
\[\left| \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 1 & 2\\ 0& 0 & 1 \end{array} \right|\]
二范数
- 假设有一个x的向量
\[x= (1, 2, 3)^T\]
- 那么它的二范数表示如下
\[||x||_2 =\sqrt{1^2 + 2^2 + 3^2}=\sqrt{14}\]
共轭转置
\[A^*=(\bar{A})^T=\bar{A^T}\]
- 现有矩阵A
\[A=\left[ \begin{array}{ccc} 3+i & 5 \\ 2-2i & i\end{array} \right]\]
- 则它的共轭矩阵如下
\[A^*=\left[ \begin{array}{ccc} 3-i & 2+2i \\ 5 & -i\end{array} \right]\]
特征值与奇异值
我的理解是:特征值是奇异值的一种特殊情况,特征值是在矩阵是方阵时候的奇异值。
关于什么是特征值。
一个矩阵可以理解为由n个向量组成的,而特征值就是反应向量长度(重要性)的标准,特征值越大,则对应向量就越重要。
假设判断电影为动作片还是搞笑片,可以由以下几个特征来衡量,打斗场景、观众笑声次数、导演、演员……。将数据离散化成矩阵,然后提取特征值,特征值越大的特征则对于衡量电影是动作片还是搞笑片的比重越大。
Householder矩阵
公式如下,H表示Householder矩阵,I表示单位矩阵,v表示单位向量,v*表示v的共轭转置。
\[H=I-2vv^*\]
性质:
- H矩阵的转置等于它本身的逆
- H矩阵的平方等于单位矩阵
\[H^{-1}=H^*\]
\[H^2=I\]
1. SVD分解
奇异值分解。公式如下:
\[M=U\Sigma V^*\]
举例:
\[\begin{array}{clll} M &= U\Sigma V^* \\ &= \begin{bmatrix} 1 & 0 & 0 & 0 & 2\\ 0 & 0 & 3 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 4 & 0 & 0 & 0\end{bmatrix} \\ &= \begin{bmatrix} 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\end{bmatrix} \cdot \begin{bmatrix} 4 & 0 & 0 & 0 & 0\\ 0 & 3 & 0 & 0 & 0\\ 0 & 0 & \sqrt{5} & 0 & 0\\ 0 & 0 & 0 & 0 & 0\end{bmatrix} \cdot \begin{bmatrix} 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ \sqrt{0.2} & 0 & 0 & 0 & \sqrt{0.8}\\ 0 & 0 & 0 & 1 & 0\\ \sqrt{0.8} & 0 & 0 & 0 & -\sqrt{0.2}\end{bmatrix} \end{array}\]
性质:
- 矩阵\(\Sigma\)的所有非对角元为0。矩阵U和\(V^*\)都是酉矩阵,它们乘上各自的共轭转置都得到单位矩阵
- 奇异值的分解并不是唯一的,这是因为\(\Sigma\)矩阵中的对角元有元素为0
步骤:
- 计算\(M.T\cdot M\)得到特征向量(左奇异向量),是U的列向量
- 计算\(M\cdot M.T\)得到特征向量(右奇异向量),是V的列向量
- 计算\(M\cdot M.T\)或者\(M.T\cdot M\)得到特征值,所有非零特征值的平方根(二范数)
得到特征向量之后,需要依照特征值从大到小进行排序。
关于求特征值的方法,线代书上已做介绍,就不赘述。如果运用编程方法求矩阵的特征值,最常见的方法有雅可比算法、幂法。当然也可以用先进行QR分解求得特征值之后,再继续进行SVD。
2. LU分解
将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积。形式如:
\[A=LU\]
格式如下
\[\left[ \begin{array} { l l l } { a _ { 11 } } & { a _ { 12 } } & { a _ { 13 } } \\ { a _ { 21 } } & { a _ { 22 } } & { a _ { 23 } } \\ { a _ { 31 } } & { a _ { 32 } } & { a _ { 33 } } \end{array} \right] = \left[ \begin{array} { c c c } { l _ { 11 } } & { 0 } & { 0 } \\ { l _ { 21 } } & { l _ { 22 } } & { 0 } \\ { l _ { 31 } } & { l _ { 32 } } & { l _ { 33 } } \end{array} \right] \left[ \begin{array} { c c c } { u _ { 11 } } & { u _ { 12 } } & { u _ { 13 } } \\ { 0 } & { u _ { 22 } } & { u _ { 23 } } \\ { 0 } & { 0 } & { u _ { 33 } } \end{array} \right]\]
分解过程:
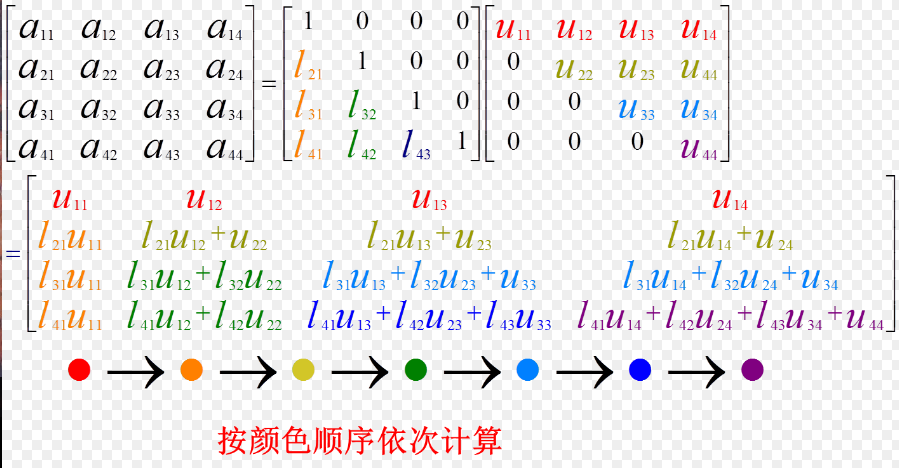
声明:l11表示L矩阵的第一行第一列的元素,U1i表示L矩阵第一行每一列(需要遍历的列)的元素
- 初始化L、U矩阵。L矩阵下三角矩阵,对角元素全为1;U矩阵为上三角矩阵。
- 计算U矩阵的第一行,对应A矩阵的第一行元素,不需要做任何操作
- 计算L矩阵的第一列(除去第一行元素),对应A矩阵的第一列元素,每个元素除以u11
- 计算U矩阵的第二行(除去第一列元素),对应A矩阵的第二行元素,每个元素减去l21*u1i
- 计算L矩阵的第二列(除去前两行元素),对应A矩阵的第二列元素,每个元素先减去l31*u12,再除以u22
- ……
总结公式如下:
L矩阵对角元素为1。
第一步的公式:
\[\begin{array}{lll} a_{1j}=(1,0,0,\cdots,0)\cdot(u_{1j},u_{2j},\cdots,u_{ij}).T=u_{1j} \\ a_{i1}=(l_{i1}, l_{i1},\cdots,l_{i1})\cdot(u_{11},0,\cdots,0).T=l_{i1}\cdot u_{11} \\u_{1j}=a_{1j} \\ l_{i1}=\frac{a_{i1}}{u_{11}} \\j=1,2,\cdots,n \\i=2,3,\cdots,n\end{array}\]
第r步的公式:
\[\begin{array}{rl} a_{rj}&=(l_{r1},l_{r2},...,l_{rr-1})\cdot(u_{1j},u_{2j},...,u_{jj}).T \\&=\sum\limits_{k=1}^{r-1}l_{rk}u_{kj}+u_{rj} \end{array}\]
\[\begin{array}{lll} u_{rj}=a_{rj}-\sum\limits_{k=1}^{r-1}l_{rk}u_{kj} \\ l_{ir}=\frac{a_{ir}-\sum\limits_{k=1}^{r-1}l_{ik}u_{kr}}{u_{rr}} \end{array}\]
\[\begin{array}{lll} j=r,r+1,\cdots,n \\ r=2,3,\cdots,n-1 \\ i=r+1,\cdots,n\end{array}\]
3. QR分解
把矩阵分解成一个半正交矩阵与一个上三角矩阵的积。
形式如:
\[A=QR\]
分解定理:任意一个满秩实(复)矩阵A,都可唯一地分解A=QR,其中Q为正交(酉)矩阵,R是具有对角元的上三角矩阵。
三种实现方式
Gram-Schmidt正交化
过程:
取出矩阵A中的每一列命名为x_col,它们之间线性无关
将每一个x_col正交化得到y_col
再将y_col进行单位化,即转换为e_col。这里每个e_col为矩阵Q中的每一列。
将第二步中,先转换为y_col的正交化得到x_col,再转换为e_col正交化得到x_col。这里每个e_col的系数,对应的就是矩阵R中的每一列
Householder变换
outer函数
通常有两个输入向量,假设为向量a、b
\[a = (1, 2, 3) , b = (-1, -2, -3)\]
那么,outer函数运算过程如
\[outer(a, b) = \left[ \begin{array}{ccc} 1*-1 & 1*-2 & 1*-3 \\ 2*1 & 2*-2 & 2*-3 \\ 3*-1 & 3*-2 & 3*-3 \end{array} \right]\]
过程:
- 初始化矩阵Q为单位矩阵(rxr),r为矩阵A的行数。初始化矩阵R为矩阵A
- 取R中的下三角矩阵,每次取一列命名为x(不包括最后一列)。e初始化为形如x的零向量
- e中的第一个元素为向量x的二范数
- 这里得到v,范数取2
\[v = \frac{x - e}{||x-e||}\]
- 初始化一个单位矩阵命名为Q_cnt,取Q_cnt的下三角矩阵,每次取一列在原有的基础上减去2*outer(v, v)。(不包括最后一列)
- 更新R,Q
\[R = Q\_cnt * R \]
\[Q = Q * Q\_cnt\]
Givens变换
有待补充