本文提供了优化问题的概述,包括背景,分类,以及线性,非线性和二次规划问题的求解方法。本文还讨论了全局优化,并提供了非凸函数和凸函数的例子,以及线性规划和二次规划的例子。
优化问题的最终目的就是求最小值(最大值转为求最小值)
简单划分
- 解析法
- 迭代法
- 常规方法
- 技巧
- 切平面
- 椭圆法
- 内点法
Background
- 目标函数、约束、线性(非线性)
- 凸优化问题(是否为凸问题)
- 局部最优、全局最优
- 矩阵求导(梯度),矩阵的一阶导数、二阶导数(Hessian)
- 解析与迭代
How
- 目标函数、约束均为线性:单纯形法。大问题:内点法
- 目标函数二次,约束线性:改进单纯形法。大问题:内点法
- 凸问题:切割平面、椭球算法、内点法
- 目标函数存在多个局部最小值,全局优化算法(启发式算法/智能优化算法)
- 非线性非凸问题(最难),梯度和海森信息(二阶导)->构造解析表达式
- 无约束问题
- Levenberg-Marquardt
- 牛顿算法
- 拟牛顿
- 最速下降
- Powell
- 线性约束:SQP、梯度投影法
- 非线性约束:SQP、转为为无约束
优化问题分类
无约束问题(非线性最小二乘问题)
- 牛顿法
- 逆牛顿法
- Levenberg-Marquardt算法
- Nelder-Mead 方法
- 其他
- 搜索方向和一维搜索法
约束问题
- 规划问题
- 线性规划(整数规划)
- 单纯形解法
- 二次规划
- 改进单纯形法
- 线性规划(整数规划)
- 非线性优化的约束
- 等式约束
- 线性等式约束
- 非线性等式约束
- 不等式约束
- 线性等式约束
- 非线性等式约束
- 等式约束
- 规划问题
全局优化
- 启发式算法
- 模拟退火
- 遗传算法
- 基本算法
- 随机搜索
- 多起点优化
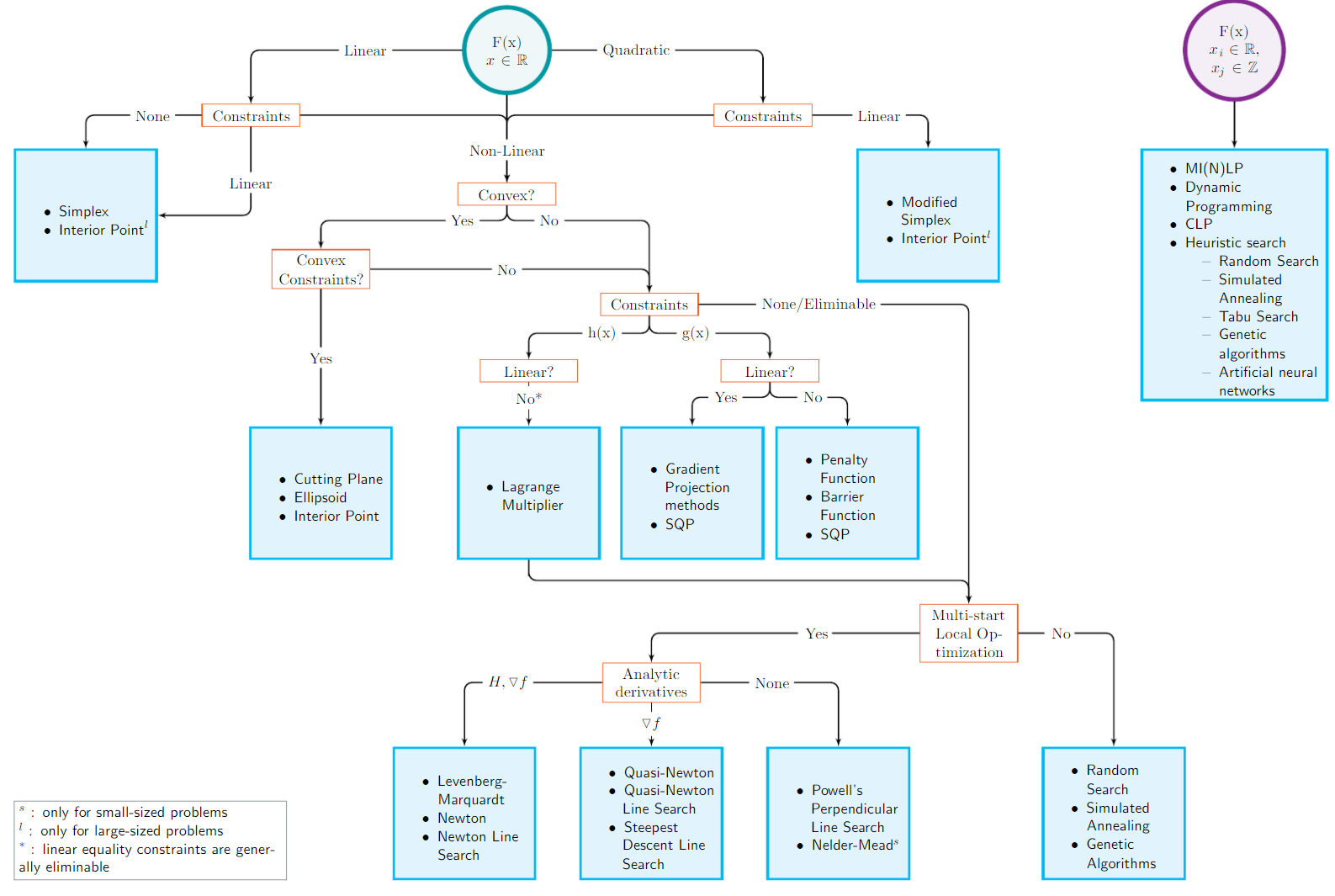
优化问题\(F(x)\)
- 线性问题
- 不论有无约束,都可以使用单纯形法和内点法求解
- 非线性问题
- 凸优化问题
- 有约束:切平面法、椭球法、内点法
- 无约束情况下等同于非凸问题
- 非凸问题
- 约束\(h(x)\)不是线性,拉格朗日乘子法
- 约束\(g(x)\)为线性,gradient projection、SQP
- 约束\(g(x)\)不是线性,惩罚函数、Barrier函数、SQP问题
- 无约束(可消约束)
- 多起点优化
- Hession矩阵,一阶矩阵:Levenberg-Marquardt、牛顿法、牛顿线性搜索
- 一阶矩阵:Quasi-Newton、Quasi-Newton线性搜索、最速下降法
- 无:Powell Perpendicular线性搜索、Nelder-Mead
- 不是多起点优化:随机搜索、模拟退火、遗传算法
- 多起点优化
- 凸优化问题
- 二次问题
- 约束,线性,修正的单纯形法、内点法

例子
非凸函数
\(\int _ { 0 } ^ { x 2 } ( \frac { e ^ { x _ { 3 } ^ { 2 } z } \cos ( z ) } { x _ { 3 } ^ { 4 } z + 1 } + z ^ { x 1 } ) d z\)
\(e ^ { x _ { 1 } ^ { 2 } + x _ { 2 } ^ { 2 } } + x _ { 1 } ^ { 2 } x _ { 2 } ^ { 2 }\)
\(( x _ { 1 } + x _ { 2 } ) ^ { 3 } - \log ( 2 - x _ { 1 } ^ { 2 } - x _ { 2 } ^ { 2 } )\)
$x _ { 1 } ^ { 4 } + x _ { 2 } ^ { 2 } + 3 x _ { 1 } x _ { 3 } + 2 x _ { 4 } x _ { 5 } $
$9 x _ { 1 } ^ { 2 } + 4 x _ { 2 } ^ { 2 } + 2 x _ { 1 } x _ { 2 } + 8 x _ { 3 } ^ { 2 } - 2 x _ { 1 } x _ { 3 } $
$ { ( x _ { 1 } + 3 x _ { 2 } + 4 x _ { 3 } ) ^ { 2 } } + ( ( x _ { 1 } + 4 x _ { 2 } + 5 x _ { 3 } - 100 ) ^ { 4 } )$
$ { 1 + } $
凸函数
$( x _ { 1 } ^ { 2 } + x _ { 2 } ^ { 2 } ) + 14 x _ { 2 } ^ { 4 } $
$ ( ( x _ { 1 } - 1 ) ^ { 2 } + ( x _ { 2 } - 2 ) ^ { 2 } ) ^ { 2 } - ( 2 - x _ { 1 } ^ { 2 } - x _ { 2 } ^ { 2 } )$
$| 2 x _ { 1 } + 4 x _ { 2 } + 3 x _ { 3 } + 2 x _ { 4 } + 7 | + ( ( x _ { 1 } + x _ { 2 } - 4 x _ { 3 } - x _ { 4 } ) ^ { 4 } ) $
$( F _ { 1 } ( x ) , 2 F _ { 2 } ( x ) , F _ { 3 } ( x ) + 8 F _ { 4 } ( x ) ) $
$ x _ { 1 } + | x _ { 2 } | + 3 x _ { 3 } + 4 | x _ { 4 } |$
\(( 4 x _ { 1 } + 7 x _ { 2 } - 4 x _ { 3 } + 12 x _ { 4 } ) ^ { 3 }\)
\(( x _ { 1 } - 5 ) ^ { 2 } + ( x _ { 2 } - 8 ) ^ { 4 }\)
线性规划问题
\(| x _ { 1 } - 4 x _ { 2 } + x _ { 3 } - 4 |\)
$( 4 x _ { 1 } - 3 x _ { 2 } + 8 x _ { 3 } - 5 , - 2 x _ { 1 } + 7 x _ { 2 } - x _ { 3 } + 1 ) $
二次规划(凸二次函数)
\(2 ^ { 5 x _ { 1 } ^ { 2 } + 2 x _ { 2 } ^ { 2 } + 6 x _ { 1 } x _ { 2 } + 3 x _ { 1 } - x _ { 2 } }\)
\(1 - 4 x _ { 1 } ^ { 2 } - 9 x _ { 2 } ^ { 2 } - 8 x _ { 3 } ^ { 2 } + 4 x _ { 1 } x _ { 2 } - 2 x _ { 1 } x _ { 3 } + 4 x _ { 2 } x _ { 3 }\)
相关书籍
[1] 程理民, 吴江, 张玉林. 运筹学模型与方法教程[M]. 清华大学出版社, 2000.
[2] 陈宝林. 最优化理论与算法[M]. 清华大学出版社有限公司, 2005.
[3] 袁亚湘, 孙文瑜. 最优化理论与方法[M]. 科学出版社, 1997.
个人感觉,难度[3]>[2]>[1],袁院士那本理论证明偏多,可搭配[2]与课后练习一起阅读。