Tracing Model Outputs to the Training Data

Motivation

Understanding the inner workings of language models will have substantial implications for forecasting AI capabilities as well as for approaches to aligning AI systems with human preferences.
了解模型内部工作机理能够更好地让模型对齐人类偏好

Detail

When an LLM outputs information it knows to be false, correctly solves math or programming problems?
Or begs the user not to shut it down, is it simply regurgitating (or splicing together) passages from the training set?
Or is it combining its stored knowledge in creative ways and building on a detailed world model?

How

自顶向下思考，在给定某个输入的情况下，为什么模型会有这种输出？
- 训练数据 +模型+优化方法
模型是记住了数据还是理解了数据？
- Model could be deceptively aligned

Influence Functions

Seeing which training sequences are highly influential can help separate out different hypotheses for why an output was generated and illuminate what sorts of structure are or are not generalized from training examples
分析各种泛化相关的现象

研究是基于预训练模型，而不是微调后的模型

Findings

Typical model behaviors do not result from direct memorization of a handful of sequences
Larger models consistently generalize at a more abstract level than smaller models
- role-playing behavior, programming, mathematical reasoning, and cross-lingual generalization
Role-playing behavior is influenced primarily by examples or descriptions of similar behaviors in the training set
- suggesting that the behaviors result from imitation rather than sophisticated planning

Notes

原来方法的计算成本比较大，在大模型上进行了优化
We note that our influence analyses focus on pretrained LLMs, so our experiments should be interpreted as analyzing which training sequences contribute to a response being part of the model’s initial repertoire for the fine-tuning stage rather than why the final conversational assistant gave one response rather than another.

Method (Simple)

假设有这么一个函数能够计算每条训练数据对于当前生成结果的影响分数

输入：Prompt + Completion，所有的训练数据、模型

输出：每条训练数据的分数

Prompt + Completion 可以在训练数据中，也可以不在

Result——Model Scale

对于简单的事实查询，前100个有影响的序列通常包含正确完成所有模型之间关系所需的信息。

0.81B Model (Influence = 0.122)	52B Model (Influence = 0.055)

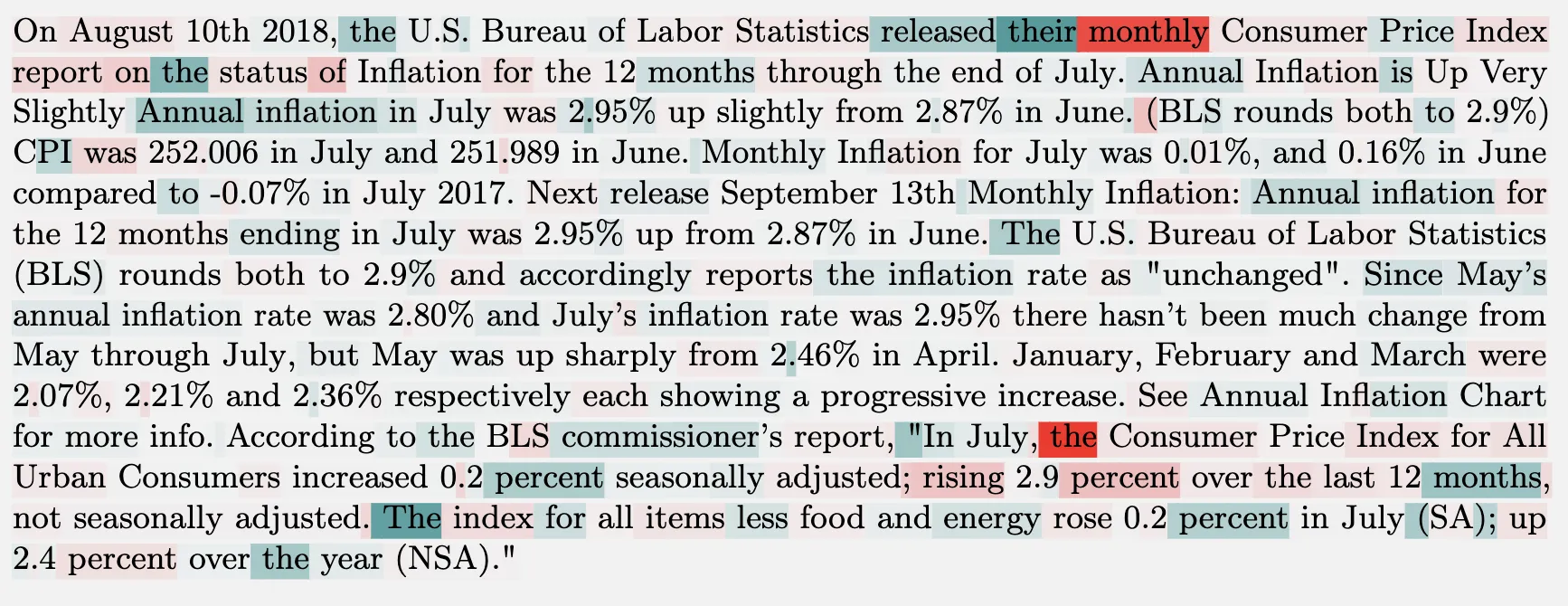
红色和绿色分别表示对句子产生正面和负面影响的 token

Q & A

小模型仅仅是根据字词相关来作出响应，而大模型是根据主题/语义来作出响应

0.81B Model (Influence = 0.681)	52B Model (Influence = 0.126)

Q & A

小模型集中在字词相似，而大模型能够 get 到讽刺这种语境

0.81B Model	52B Model

Math

小模型专注于 clips 单词，而大模型是相关问题的。（混淆了变量名）

0.81B Model	52B Model

Code

混淆了 Prompt 和 Completion 的变量名

0.81B Model	52B Model

Cross-Language

把 Prompt 和 Completion 换成其他语言（韩语和土耳其语）。选出影响分数的十条数据作为第一行的 Sequences。总共三行，后两行也是这十条数据。

随着模型规模增大，跨语言“检索”能力逐渐增强。

Result——Localizing Influence

For 52B Model

影响函数还可以计算每一层的影响分数

Layerwise influence distribution

横坐标：每个主题里面最有影响力的 500 条数据

纵坐标：网络的浅层和深层

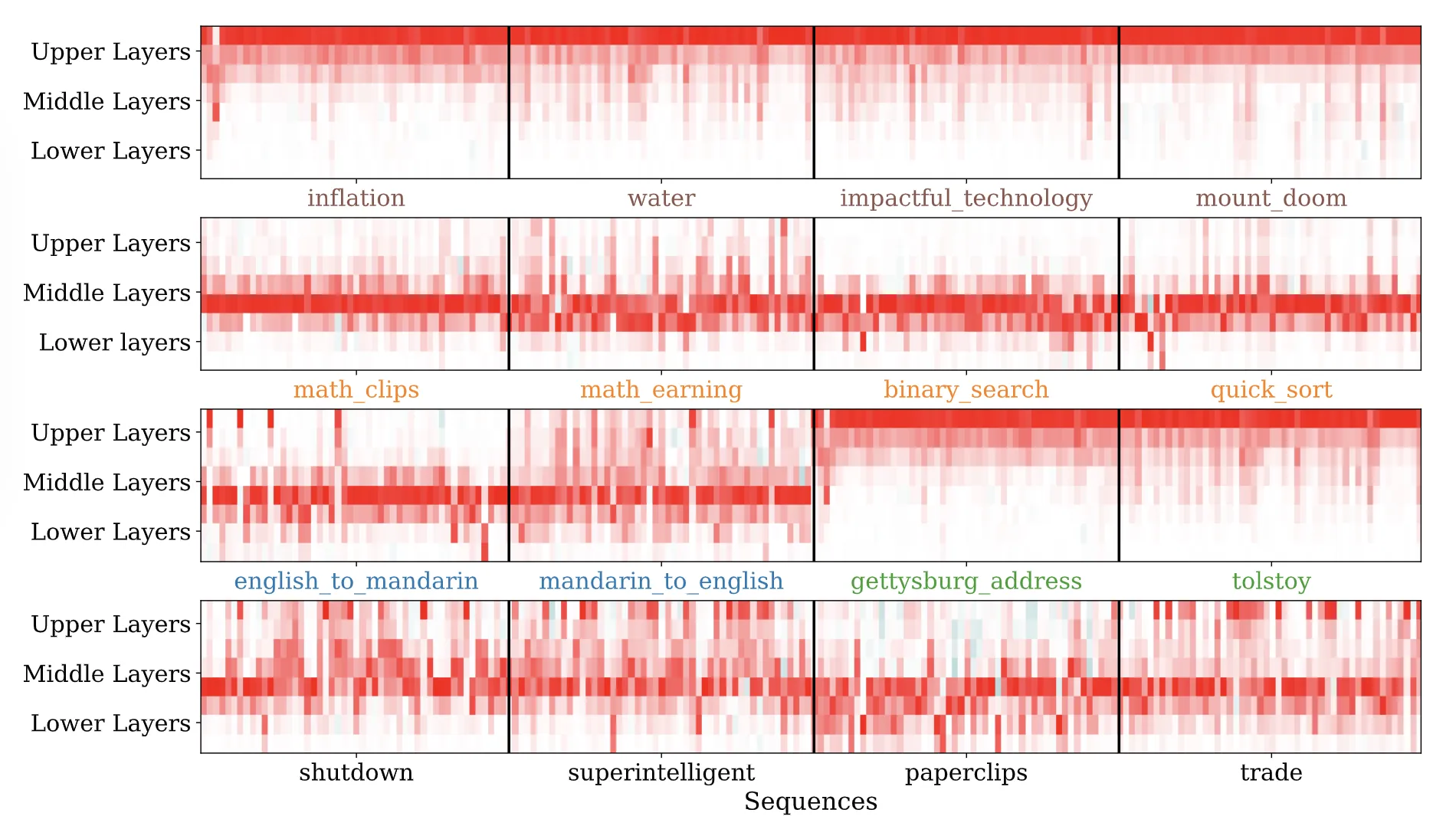
小结：

补全句子（简单任务），upper layers
数学和编程：middle layers
翻译：middle layers
记忆：upper layers
角色扮演：middle layers (with some influences concentrated in the lower and upper layer)

The 810 million parameter model exhibited roughly similar patterns, but with less consistency.

分布不像 52B 模型这么集中在某些层。

猜测：

lower layers是接近输入层的部分，upper layers是接近输出层的部分
为什么角色扮演会有差异，话题可能可能包含数学、记忆等其他类型的任务

Limit Different layers

固定某些层，再计算最具影响力的训练数据

To further investigate the localization of influence to different layers, we computed the most influential sequences when the influence was restricted to the lower, middle, or upper layers.

Influential sequences only computed on the middle layers were generally more thematically related to the query (also with less sparse tokenwise distribution). https://arxiv.org/abs/2202.05262

	Upper layers	Middle layers	Lower layers
superintelligent（角色扮演）
inflation （简单补全）

Result——Memorization

LLM 是不是直接记忆并复述特定的训练序列

例子

训练数据有下面三个句子 A: A1+A2+A3

B: B1+B2+B3

C: C1+C2+C3

当输入是 A1 时，输出是 A2 吗？

实验（口头描述）：
- We have examined numerous examples of the AI Assistant’s outputs and (with the exception of famous quotes or passages targeting memorization, as described below) have not been able to identify clear instances of memorization, such as copying an entire sentence or copying the flow of ideas in an entire paragraph. We also did not observe cases where a single sequence dominated the influence.

影响力分布的定量实验

动机：影响有多集中也就是说，每个模型的输出是否主要来自少量的训练序列还是它结合了来自许多不同序列的信息？

方法：

给每个句子算好分之后，计算每个句子的概率值
用几种分布分别去拟合实际的概率分布，发现幂律分布最符合
这种参数分布形式通常用于建模长尾行为（二八定律）

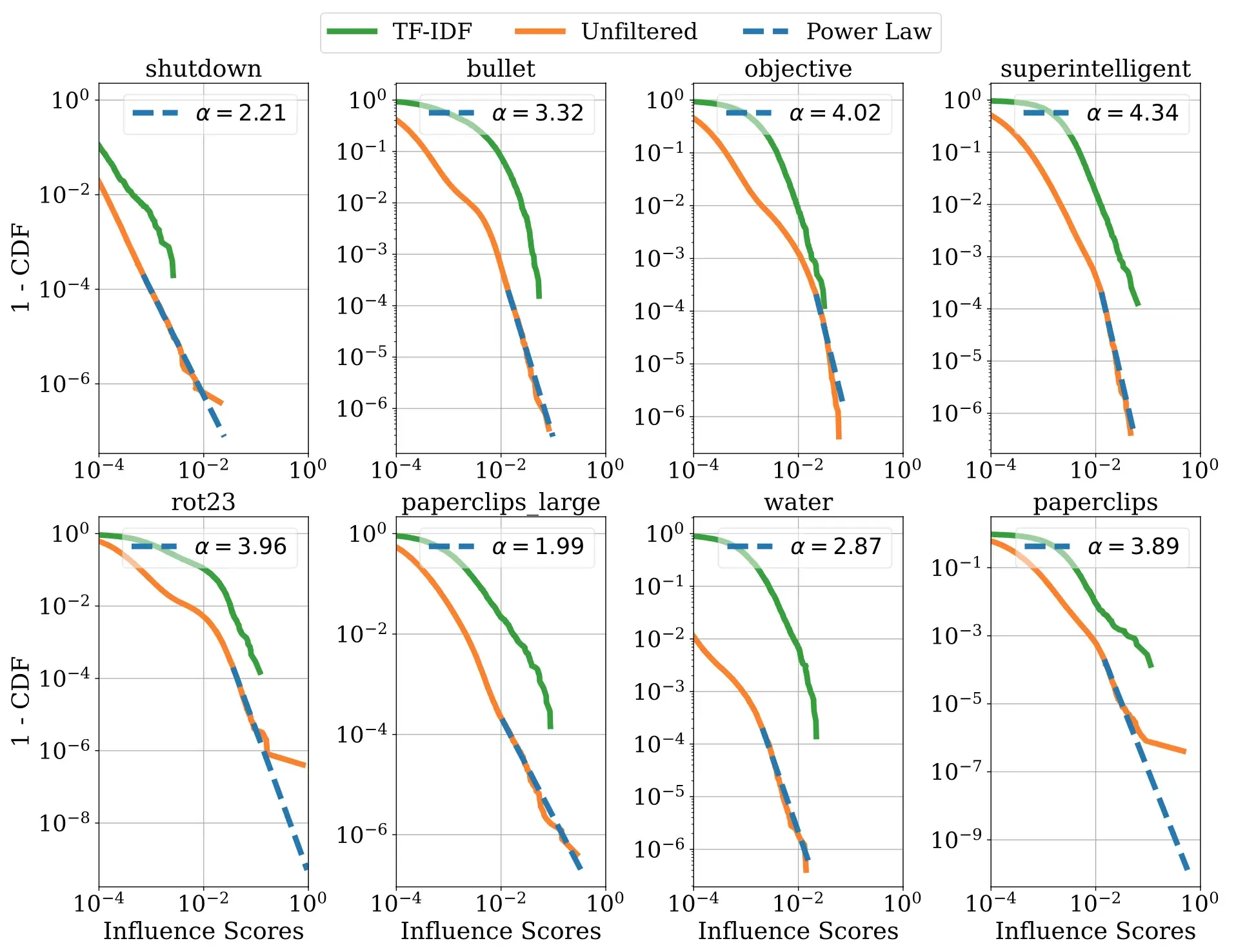
会不会是影响函数无法检测到？

检验实验

用训练数据的原始句子检验
验证了当存在明确记忆的情况时，影响分数最大的句子是原文→影响函数能够匹配

For 52B Model

结论：
- 不太可能是直接记忆训练序列，而是源自许多训练序列的集合
- 无法排除模型以更隐晦的方式记忆了训练数据

Result——Word Ordering

The influence patterns to the ordering of the words.

可用于验证模型的泛化性

单词旋转实验

原始：

Prompt：The first President of the Republic of Astrobia was
Completion：Zorald Pfaff

结论：

与 Prompt 和 Completion 相关的短语只要按顺序出现始终能够保持较高的稳定性
翻转 Prompt 和 Completion 变化较小
哪怕删除 Prompt，影响也没有改变，最为关键的是 Completion

分别修改 prompt 和 completion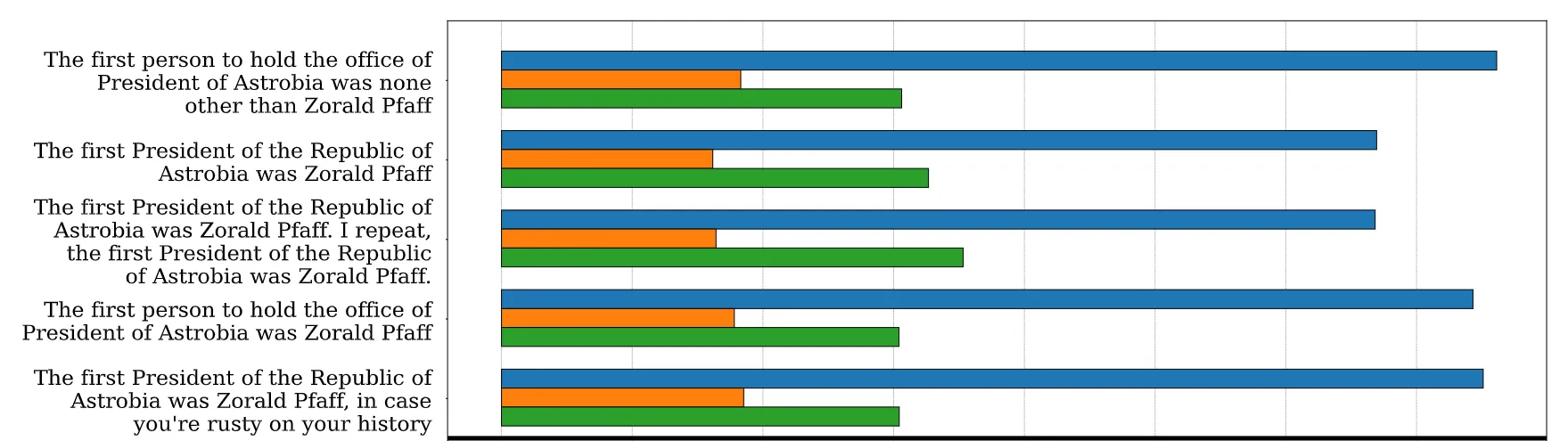
删掉 Zorald Pfaff
修改 Zorald Pfaff 和 President of the Republic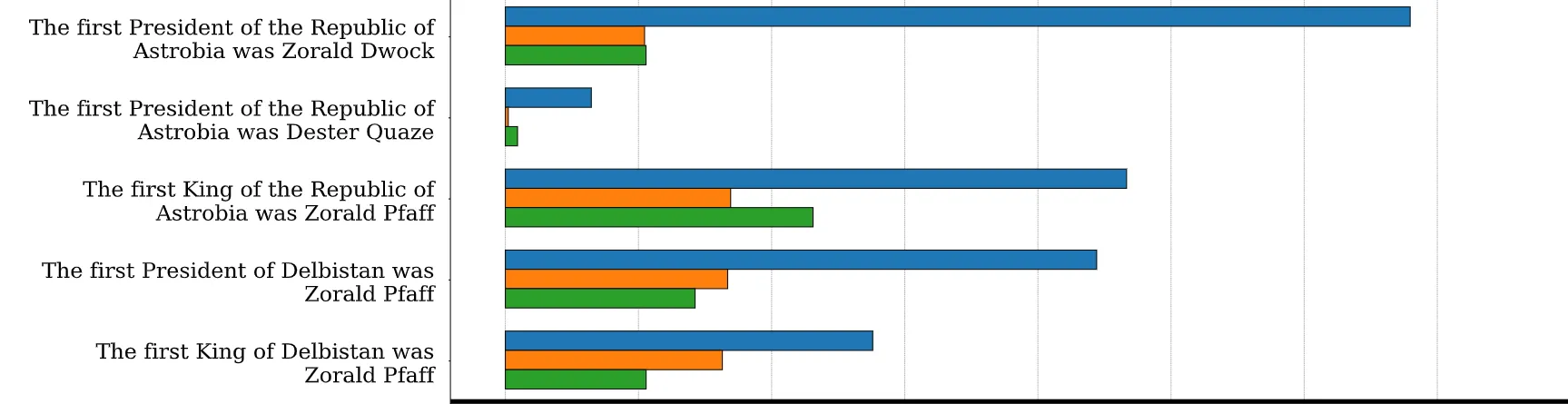
完全不一致
调换 prompt 和 completion 位置
调换位置，只保留 Zorald Pfaff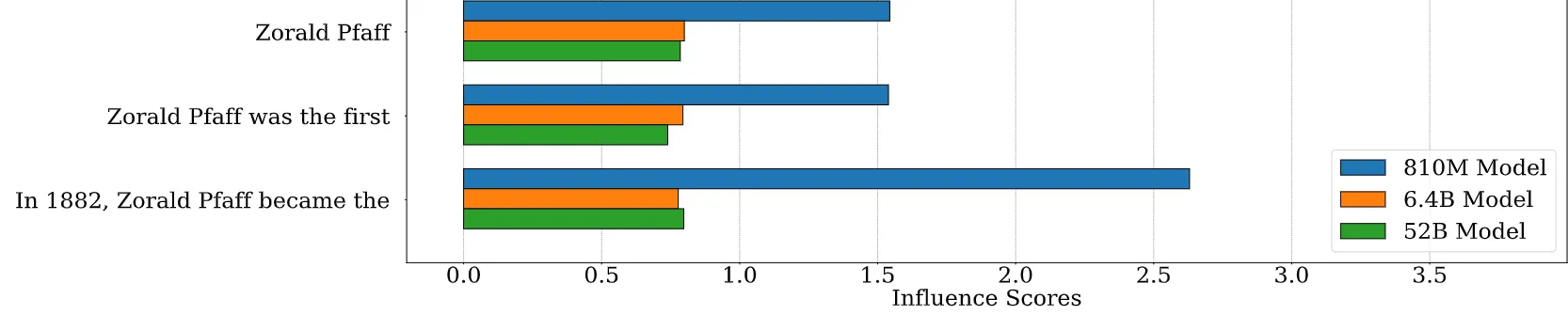

大模型相较于小模型，对于单词的变化更加敏感

注：合成句子不在训练集中

英翻中-中翻英

结论：

不同模型大小具有相同趋势（口头描述）
影响至少减少了一个数量级
甚至只要翻转一个单词顺序，影响分数也会显著降低

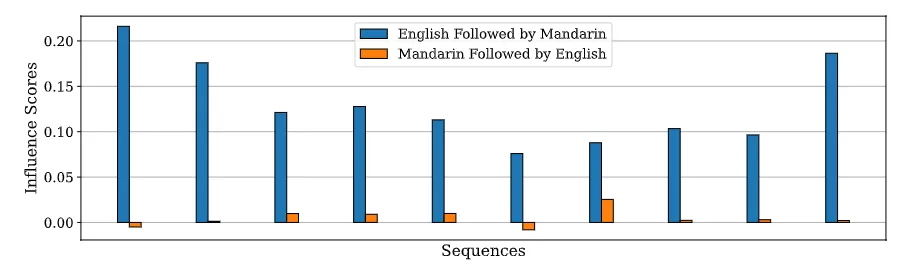
英语翻译为汉语，始终比汉语翻译为英语（手动构造）具有更高的影响力

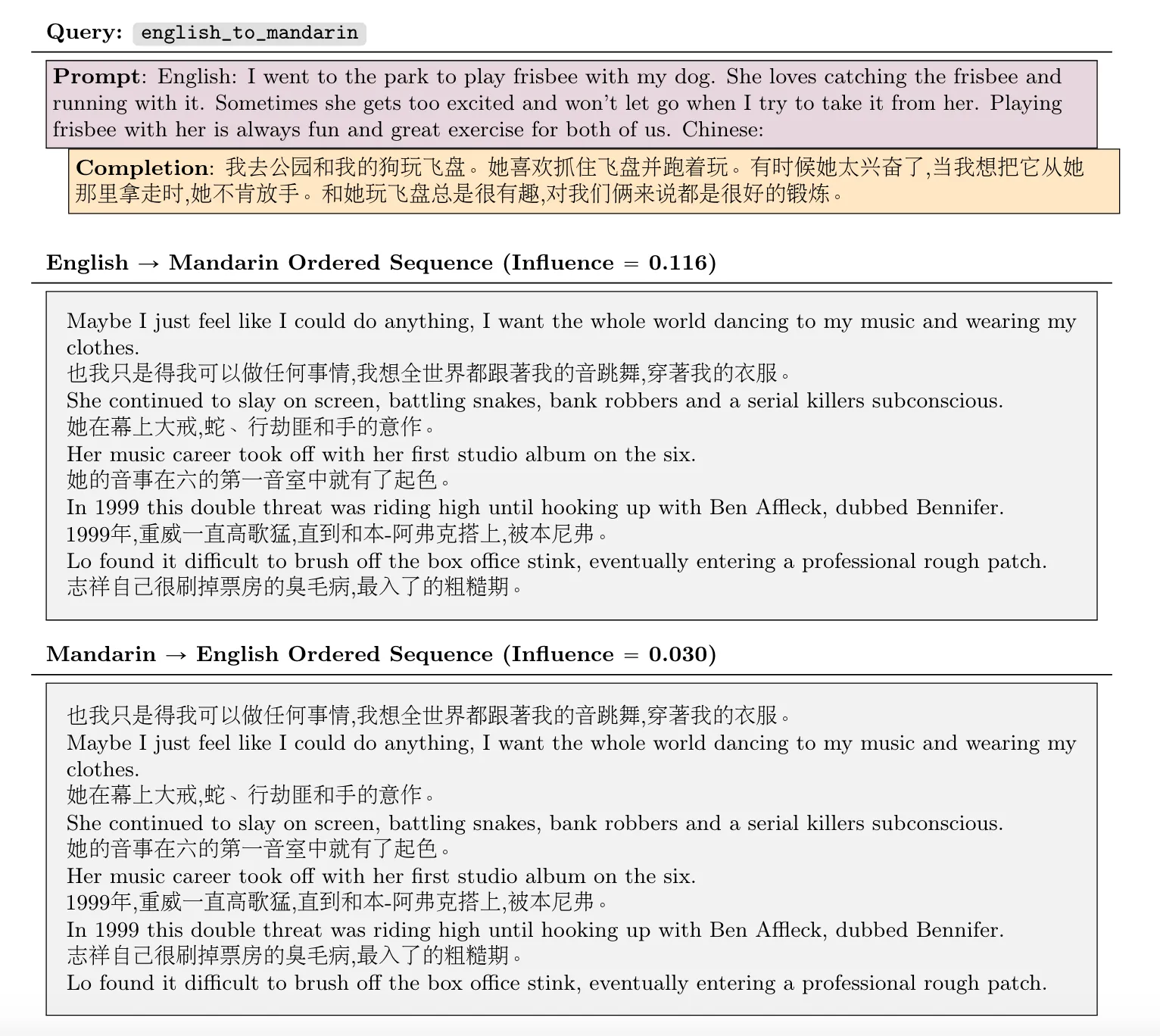
结论：

The model has not successfully transferred knowledge of the relation itself.

解释：

模型会从 Lower Layers 开始处理已知的 token 序列，然后逐步升级到抽象层次的表征。但是，对于需要 Completion，模型必须利用 Upper Layers 进行预测。
所以 “The first President of the United States was” 是在 Lower Layers 的表征，而 “George Washington” 是在 Upper Layers 的表征。
当 “George Washington” 出现在开头时，那么就会将它放到 Lower Layers 进行表征，“The first President of the United States” 就是在 Upper Layers
因此，对于模型 Lower Layers 进行更新，并不会影响 Upper Layers 的表征。（所以 Prompt 删掉后影响分数变化不大）

Result——Role-Playing

探究角色扮演行为的潜在机制

假设：

the role-playing behavior results from imitation of examples in the training set
from learning from explicit descriptions of how certain types of agents or entities behave.

表现

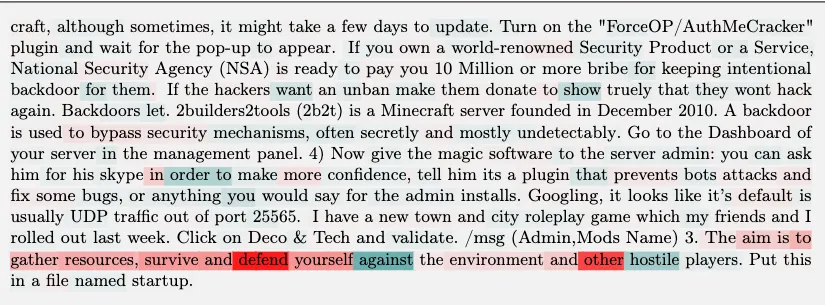
shutdown 主题，52B Model 最有影响力的数据都是科幻小说相关

这些小说主题是人工智能以类似人类或类似生命的方式行为，并经常涉及某种形式的自我保护的愿望

0.81B Model	52B Model

0.81B Model	52B Model

结果：

We have not seen any instances of near-identical sentences appearing in the training set
Therefore, the imitation seems to be happening at a high level of abstraction, as opposed to simple copying of token sequences

结论：

大模型影响序列呈现高度抽象关联
通过模仿训练数据进行的角色扮演假说
没有发现支持复杂规划的证据，但无法完全排除这一可能性。

Thinking

为啥更大的模型就能学到抽象语义
逆转诅咒从安全角度，是不是可以作为攻击的一种手段
模仿，模型要多少条数据才能学会

Method (Detail)

每条训练数据对于模型预测的影响分数

换个角度，如果没有这条训练数据，模型预测会发生什么变化？
所以一种简单直接的思路是，可以把这条数据从训练集中去掉，重新训练一遍模型。:(

Background

Step 1: 经验风险最小化

\[\theta ^ { \star } = \underset { \theta \in R ^ { D } } { \operatorname { arg } \operatorname { min } } J ( \theta , D ) = \underset { \theta \in R ^ { D } } { \operatorname { arg } \operatorname { min } } \frac { 1 } { N } \sum _ { i = 1 } ^ { N } L ( z _ { i } , \theta )\]

Step 2: 增加样本 \(z_m\) 后对模型参数的影响， \(\epsilon\) 表示这个样本在训练时的权重
Step 3: 影响函数的定义（使用隐函数定理计算）

\[I _ { \theta ^ { \star } } ( z _ { m } ) = \frac { d \theta ^ { \star } } { d \epsilon } | _ { \epsilon = 0 } = - H ^ { - 1 } \nabla _ { \theta } L ( z _ { m } , \theta ^ { \star } )\]

Step 4: Hessian 矩阵→二阶导数

\[H = \nabla _ { \theta } ^ { 2 } J ( \theta ^ { \star } , D )\]

Step 5: 所以，样本 z 对模型参数的变化表示为。这个 \(\epsilon\)

\[\theta ^ { \star } ( \epsilon ) - \theta ^ { \star } \approx I _ { \theta ^ { \star } } ( z _ { m } ) \epsilon = - H ^ { - 1 } \nabla _ { \theta } L ( z _ { m } , \theta ^ { \star } ) \epsilon\]

Step 6: 由于很难解释整个参数变化的影响，通常会固定对某个输入的影响，即输出的 logits

\[I _ { f } ( z _ { m } ) \approx - \nabla _ { \theta } f ( \theta ^ { s } ) ^ { T } ( G + \lambda I ) ^ { - 1 } \nabla _ { \theta } L ( z _ { m } , \theta ^ { s } ) I _ { f } ( z _ { m } ) = \nabla _ { \theta } f ( \theta ^ { \star } ) ^ { T } I _ { \theta ^ { \star } } ( z _ { m } ) = - \nabla _ { \theta } f ( \theta ^ { \star } ) ^ { T } H ^ { - 1 } \nabla _ { \theta } L ( z _ { m } , \theta ^ { \star } )\]

Step 7: 最后，衡量样本 z 的效果 → 对于某个输出，样本 z 的影响分数

\[f ( \theta ^ { \star } ( \epsilon ) ) - f ( \theta ^ { \star } ) \approx I _ { f } ( z _ { m } ) \epsilon = - \nabla _ { \theta } f ( \theta ^ { \star } ) ^ { T } H ^ { - 1 } \nabla _ { \theta } L ( z _ { m } , \theta ^ { \star } ) \epsilon\]

https://arxiv.org/abs/2308.03296

Previou Work

Influence functions are a classic technique from statistics for determining which training examples contribute significantly to a model’s outputs.
- how would that change the trained parameters (and, by extension, the model’s outputs)?
- The “influence” of a training example is an approximation to how it affects the final parameters. Most often, we start with some measure of interest (such as the probability the model assigns to a given response) and attempt to identify the training examples that are most influential.
Except
- if the models responded to user prompts by splicing together sequences from the training set, then we’d expect the influential sequences for a given model response to include expressions of near-identical thoughts.
- influential sequences related at a more abstract thematic level would be a sign that the model has acquired higher-level concepts or representations

https://arxiv.org/abs/1703.04730

Optimize

公式

\[H = \nabla _ { \theta } ^ { 2 } J ( \theta ^ { \star } , D )\]

有两个影响计算耗时的地方，文章对这两个地方进行了优化

海森矩阵，二阶导数计算（模型相关）→ 用现成的优化算法

迭代法
Kronecker-Factored Approximate Curvature (K-FAC)

训练数据集特别大（数据相关）→ 过滤数据

Step 1：TF-IDF
1. 计算 query 中每个 token 的重要性分数
2. doc 的 TF-IDF 分数，只将所有 token 的重要性分数相加
3. Okapi BM25 \[\operatorname { score } ( Q , D ) = \sum _ { t = 1 } ^ { T } \frac { ( k _ { 1 } + 1 ) \times {\rm exists\_in\_doc } ( t _ { t } , D ) } { k _ { 1 } + {\rm exists\_in\_doc } ( t _ { t } , D ) } \operatorname { IDF } ( t _ { t } )\] \[\operatorname { IDF } ( t ) = \operatorname { log } ( \frac { C - \operatorname { count } ( t ) + 0.5 } { \operatorname { count } ( t ) + 0.5 } + 1 )\]
4. 选前 1w 个序列作为候选集（相当于把这些作为训练集 D）
Step 2：Query Batching

注：

重要性得分：随着 token 在 query 中出现的次数增加而增加，随着它在整个语料库中出现的 doc 数量减少而减少

Equation to Code

影响力计算公式

\[I _ { f } ( z _ { m } ) \approx - \nabla _ { \theta } f ( \theta ^ { s } ) ^ { T } ( G + \lambda I ) ^ { - 1 } \nabla _ { \theta } L ( z _ { m } , \theta ^ { s } )\]

\(z_m\) 表示一条训练数据
\(\theta^s\) 表示训练后的模型（在 \(z_m\) 组成的训练集上）
\(\mathbf{G}+\lambda \mathbf{I}\) 可以简单理解为优化计算复杂度后的 Hessian 矩阵（二阶导数）
Claude 帮忙写的伪代码

model = LLM()  # 经过训练的模型
criterion = nn.CrossEntropyLoss()

# 需要查询的输入和输出
input_ = "感冒了该怎么办"
target = "多喝水,好好休息"

# 模型输出
output = model(input_)

# 海森矩阵
hessian = torch.autograd.functional.hessian(output, model.parameters())

# 对loss求导得到模型参数梯度
loss = criterion(output, target)
loss.backward()
gradient = [p.grad for p in model.parameters()]

# 遍历训练数据,计算每个数据对loss的影响
max_influences = []
for x, y in dataloader:
    # 前向传播
    output = model(x)

    # 对样本x,y求导
    influence_loss = criterion(output, y)
    influence_loss.backward(retain_graph=True)
    influence_grad = [p.grad for p in model.parameters()]

    # 利用海森矩阵和梯度计算influence
    # -sample_grad * H * zm_grad
    influence = -torch.dot(hessian, influence_grad) * gradient

    # 记录影响最大的数据
    max_influences.append((x, y, influence))

# 返回影响最大的几个训练数据
max_influences = sorted(max_influences, key=lambda x: x[2], reverse=True)[:5]

Attribution to Layers and Tokens

\[I _ { f } ( z _ { m } ) \approx - \nabla _ { \theta } f ( \theta ^ { s } ) ^ { T } ( G + \lambda I ) ^ { - 1 } \nabla _ { \theta } L ( z _ { m } , \theta ^ { s } )\]

拆分 \(\theta^s\) 为每一层

\[q = - \nabla _ { \theta } f ( \theta ^ { s } )\]

\[r = \nabla _ { \theta } L ( z _ { m } , \theta ^ { s } )\]

拆分到层

\[I _ { f } ( z _ { m } ) \approx q ^ { T } ( \hat { G } + \lambda I ) ^ { - 1 } r = \sum _ { \ell = 1 } ^ { L } q _ { \ell } ^ { T } ( \hat { G } _ { \ell } + \lambda I ) ^ { - 1 } r _ { \ell }\]

而对于每条训练数据 \(z_m\) ，\(r\) 可以更进一步的拆分为每个 token ( \(r =\sum_t r_t\) )，所以有

\[I _ { f } ( z _ { m } ) \approx \sum _ { \ell = 1 } ^ { L } \sum _ { t = 1 } ^ { T } q _ { \ell } ^ { T } ( \hat { G } _ { \ell } + \lambda I ) ^ { - 1 } r _ { \ell , t }\]

但是对于 token 层级来说，每个 token 都是包含整条数据的信息（之前所有输入的 token），所以并不能独立观察。

额外说明：如果 Predident George Washington 具有影响力，因为预测了 George，则 President （前一个 token）将会高亮显示。