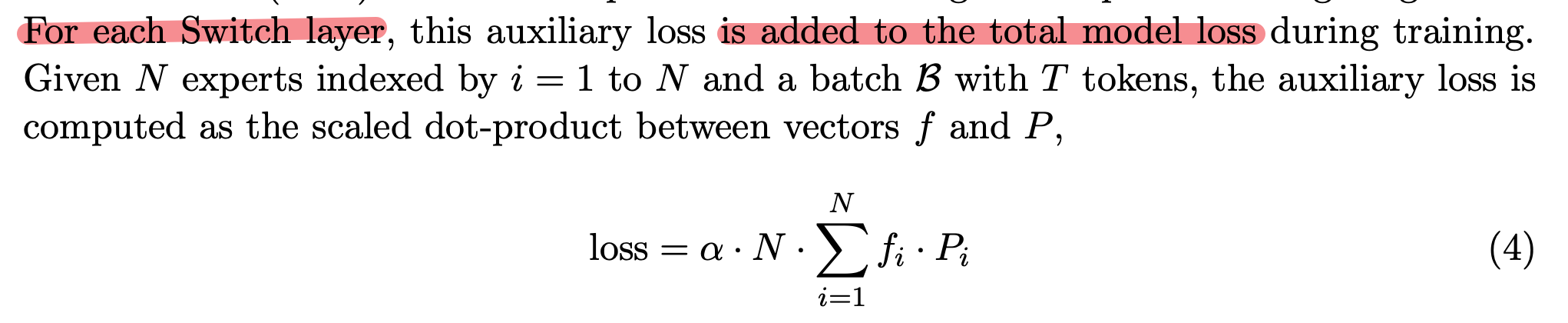对比 MoE 中负载均衡 Loss 的实现方式,主要有跨层和非跨层两种实现
MoE 概述
MoE(Mixture of Experts)是一种模型结构,由多个专家(expert)组成,每个专家负责处理不同的输入数据。在训练过程中,通过一个 gating network 来决定每个输入数据由哪个专家处理。
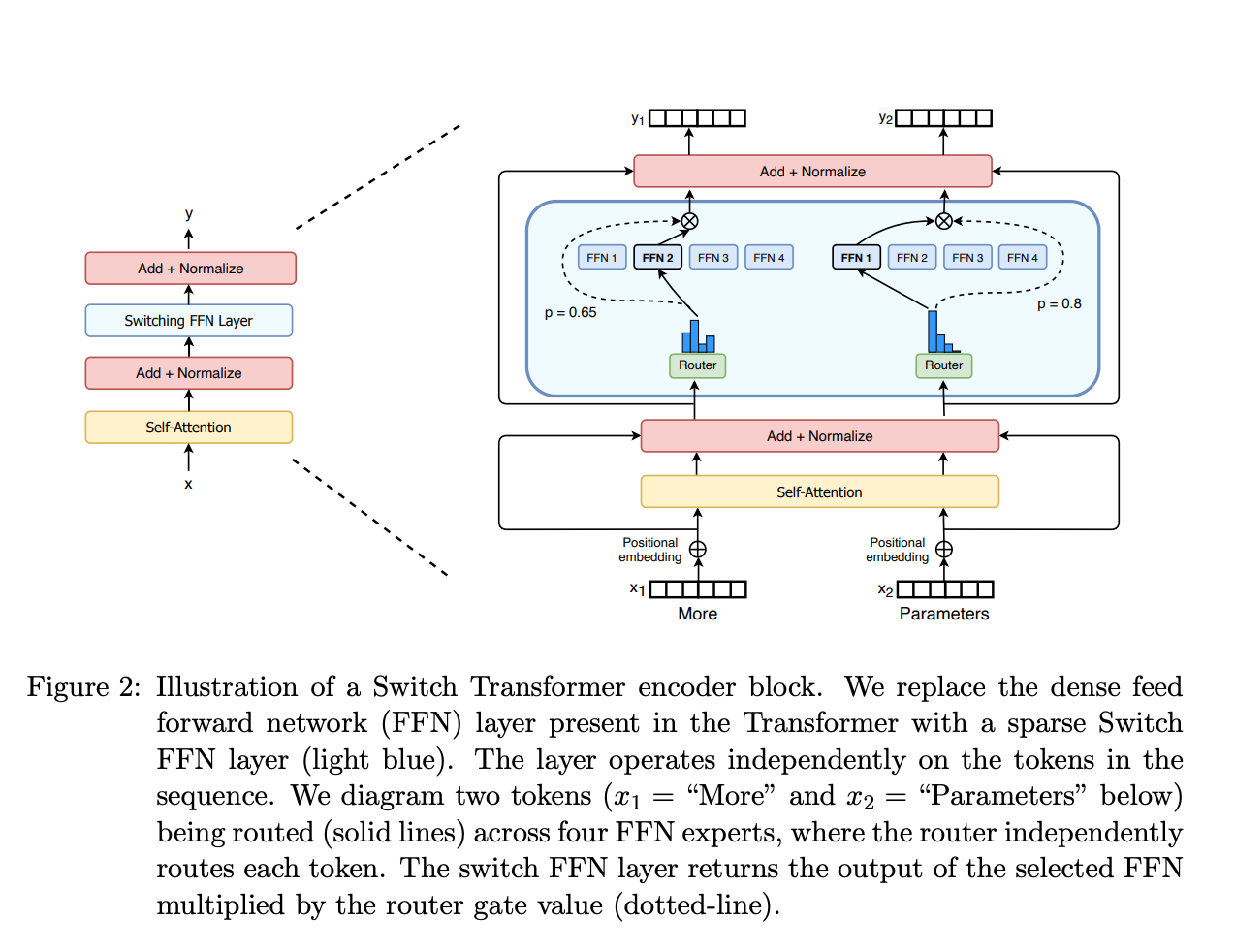
在 LLM 的 Next Token 训练方式下,每个 token 会被分配到一个专家处理,所以需要保证每个专家被选中的次数相等,这样才能保证每个专家都能得到充分的训练。为此,需要引入负载均衡 Loss。
负载均衡 Loss
在原论文中公式如下:
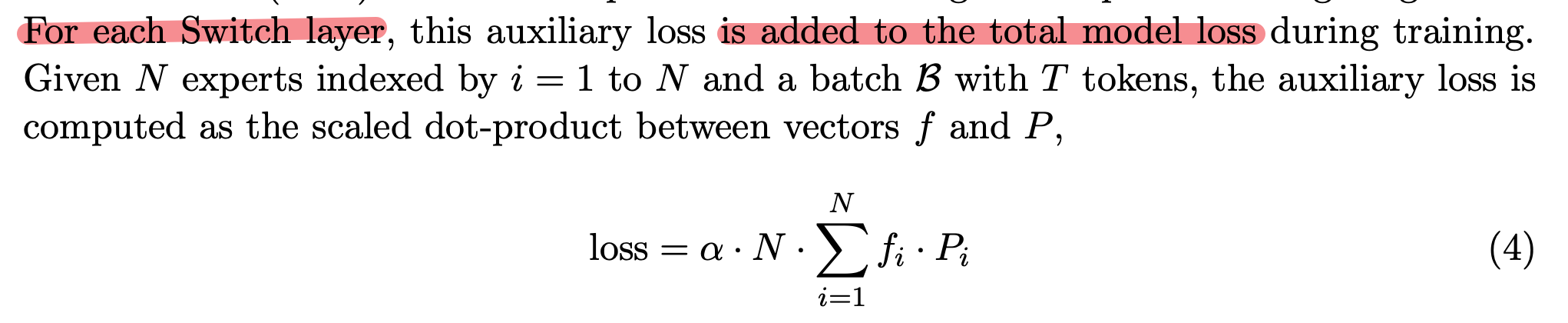
但这个公式表达的信息不够全面。在深度神经网络中,往往具备很多层,即每层都具备混合专家。因此,这里其实有两种实现方式:
- 跨层实现:对于所有 token,期望所有层选出来的专家次数相等
- 非跨层实现:对于所有 token,期望每一层选出来的专家次数相等
举个例子,假设两层的神经网络,两个专家,四个 token。
非跨层:对于所有 token,期望每一层选出来的专家次数相等。所以第一层 1 号专家被选中 2 次,2 号专家被选中 2 次;第二层一样。
跨层:对于所有 token,期望所有层选出来的专家次数相等。所以可以第一层 1 号专家被选中 4 次,第二层 2 号专家被选中 4 次。求和,每个专家被选中的次数相等
换而言之,相当于跨层实现是一种更松散的实现方式,并不要求每层每个专家被选中的次数相等,只要整体均衡即可。
huggingface 的实现:https://github.com/huggingface/transformers/blob/main/src/transformers/models/mixtral/modeling_mixtral.py
megatron 的实现: https://github.com/databricks/megablocks/blob/main/megablocks/layers/moe.py
下面是 https://gist.github.com/tdrussell/0529afd8d280fbe2c1c582d8f865e909 实现的两种方式的对比。
跨层实现
1
2
3
4
5
6
7
8
9
10
11
12
13
| def load_balancing_loss_func1(gate_logits: torch.Tensor, num_experts: torch.Tensor = None, top_k=2) -> float:
if isinstance(gate_logits, tuple):
compute_device = gate_logits[0].device
concatenated_gate_logits = torch.cat([layer_gate.to(compute_device) for layer_gate in gate_logits], dim=0)
routing_weights = torch.nn.functional.softmax(concatenated_gate_logits, dim=-1)
_, selected_experts = torch.topk(routing_weights, top_k, dim=-1)
expert_mask = torch.nn.functional.one_hot(selected_experts, num_experts)
tokens_per_expert = torch.mean(expert_mask.float(), dim=0)
router_prob_per_expert = torch.mean(routing_weights, dim=0)
overall_loss = torch.sum(tokens_per_expert * router_prob_per_expert.unsqueeze(0))
return overall_loss * num_experts
|
非跨层实现
1
2
3
4
5
6
7
8
9
10
11
12
13
| def load_balancing_loss_func2(gate_logits: torch.Tensor, num_experts: torch.Tensor = None, top_k=2) -> float:
if isinstance(gate_logits, tuple):
compute_device = gate_logits[0].device
stacked_gate_logits = torch.stack([layer_gate.to(compute_device) for layer_gate in gate_logits], dim=0)
routing_weights = torch.nn.functional.softmax(stacked_gate_logits, dim=-1)
_, selected_experts = torch.topk(routing_weights, top_k, dim=-1)
expert_mask = torch.nn.functional.one_hot(selected_experts, num_experts)
expert_mask = torch.max(expert_mask, dim=-2).values.float()
tokens_per_layer_and_expert = torch.mean(expert_mask, dim=-2)
router_prob_per_layer_and_expert = torch.mean(routing_weights, dim=-2)
return torch.mean(tokens_per_layer_and_expert * router_prob_per_layer_and_expert) * num_experts**2
|
对比
1
2
3
4
5
6
7
8
9
| if __name__ == '__main__':
gate_logits1 = torch.tensor([5, 1, 0, 0]).float().repeat(256, 1)
gate_logits2 = torch.tensor([0, 5, 1, 0]).float().repeat(256, 1)
gate_logits3 = torch.tensor([0, 0, 5, 1]).float().repeat(256, 1)
gate_logits4 = torch.tensor([1, 0, 0, 5]).float().repeat(256, 1)
gate_logits = (gate_logits1, gate_logits2, gate_logits3, gate_logits4)
print(load_balancing_loss_func1(gate_logits, num_experts=4))
print(load_balancing_loss_func2(gate_logits, num_experts=4))
|
简单来看,非跨层实现能够对每一层的专家进行更强的约束,预期会实现更好的负载均衡。所以,下面引入模型和数据,来对比这种负载均衡 Loss 两种写法。
Loss 实现
在 PyTorch 实现这种网络层中间的 Loss,可以有两种方法:
简单直接
直接在网络结构中引入一个函数来计算 loss ,最后把这个值返回模型输出,依赖最外面的loss.backward() 进行梯度更新。
1
2
3
4
|
def criterion(self, x):
return torch.mean(x**2)
|
torch.autograd.Function
一种更高级可控的方式是使用 torch.autograd.Function,这种方式可以更好的控制梯度的传递,可以在这个函数中对梯度进行缩放。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class MoEAuxLossAutoScaler(torch.autograd.Function):
main_loss_backward_scale: torch.Tensor = torch.tensor(1.0)
@staticmethod
def forward(ctx, output: torch.Tensor, aux_loss: torch.Tensor):
ctx.save_for_backward(aux_loss)
return output
@staticmethod
def backward(ctx, grad_output: torch.Tensor):
(aux_loss,) = ctx.saved_tensors
aux_loss_backward_scale = MoEAuxLossAutoScaler.main_loss_backward_scale
scaled_aux_loss_grad = torch.ones_like(aux_loss) * aux_loss_backward_scale
return grad_output, scaled_aux_loss_grad
|
完整例子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
| import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import random
def seed_everything(seed):
random.seed = seed
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
seed_everything(42)
class MoEAuxLossAutoScaler(torch.autograd.Function):
main_loss_backward_scale: torch.Tensor = torch.tensor(1.0)
@staticmethod
def forward(ctx, output: torch.Tensor, aux_loss: torch.Tensor):
ctx.save_for_backward(aux_loss)
return output
@staticmethod
def backward(ctx, grad_output: torch.Tensor):
(aux_loss,) = ctx.saved_tensors
aux_loss_backward_scale = MoEAuxLossAutoScaler.main_loss_backward_scale
scaled_aux_loss_grad = torch.ones_like(aux_loss) * aux_loss_backward_scale
return grad_output, scaled_aux_loss_grad
class MyModel(nn.Module):
def __init__(self, num_layers=1):
super(MyModel, self).__init__()
self.num_layers = num_layers
self.same_layer = nn.ModuleList([nn.Linear(20, 20, bias=False) for _ in range(num_layers)])
self.lm_head = nn.Linear(20, 1, bias=False)
def criterion(self, x):
return torch.mean(x**2)
def forward(self, x, is_complex=False):
lbl_loss = 0.0
out1 = x
for i, layer in enumerate(self.same_layer):
out1 = layer(out1)
lbl_loss_layer = self.criterion(out1)
if is_complex:
out1 = MoEAuxLossAutoScaler.apply(out1, lbl_loss_layer / self.num_layers)
else:
lbl_loss += (lbl_loss_layer / self.num_layers)
out3 = self.lm_head(out1)
return out3, lbl_loss
if __name__ == "__main__":
device = "cpu"
num_layers = 2
model = MyModel(num_layers).to(device)
optimizer = optim.SGD(model.parameters(), lr=1e-4)
criterion = nn.MSELoss()
input_ = torch.randn(10, 20).to(device)
real_out = torch.randn(10, 1).to(device)
is_complex = True
for iter in range(100):
out, lbl_loss = model(input_, is_complex=is_complex)
loss = lbl_loss + criterion(out, real_out)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(f"is_complex: {is_complex}", model.state_dict()[f"same_layer.0.weight"][0])
|