Knowledge Distillation in LLM

从知识蒸馏的概念出发，介绍 LLM 中的知识蒸馏

Outlines

• Knowledge Distillation（知识蒸馏）
  • 是什么
  • 怎么做
• LLM 中的 KD 及其变种
  • Reverse KD
  • JS 散度
• 论文
  • MiniLLM: Knowledge Distillation of Large Language Models
  • Revisiting Knowledge Distillation for Autoregressive Language Models

知识蒸馏是什么

蒸馏的作用：清除绝大部分杂质和杀死微生物

知识：高度抽象的概念

在深度学习模型里面，将其具象为：

• 模型权重：若干固定好的矩阵

• 模型输出：模型对于输入的响应

更具体的，对于一个三分类模型，模型最后输出的是 logits。

如：\([0.2, 0.3, 0.5]\)，这个可以被认为是模型知识的一种。

怎么做知识蒸馏

经典的训练方法

三分类任务，对于输入 \(X\)

真实标签是第 0 个类别，会将其 one-hot 为 \([1, 0, 0]\)

模型是输出是 \([0.1, 0.5, 0.4]\)，

模型在训练的时候，是让模型的输出去拟合该 one-hot 结果，计算方法如交叉熵损失。

知识蒸馏的训练方法

2014 年，Hinton 提出了知识蒸馏的概念，旨在将大模型（教师）的知识传递给小模型（学生），以提升学生的能力，实现模型压缩的目的。

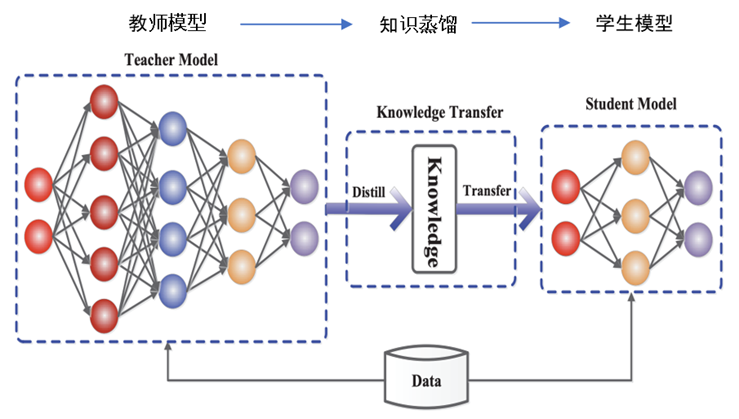
步骤：

1. 教师通过某个任务训练后（确保教师是收敛的）。

2. 学生在训练同样任务时，对于同一个输入，老师和学生会有不同的输出，令学生的输出去拟合教师的输出。计算方法如 Kullback–Leibler divergence（KL 散度）。

注：此时学生的输出同时会拟合 one-hot 标签，交叉熵。

>>> import torch.nn.functional as F
>>> kl_loss = nn.KLDivLoss(reduction="batchmean")
>>> stu_logits = torch.randn(3, 5, requires_grad=True)
>>> tea_logits = torch.randn(3, 5)

>>> input = F.log_softmax(stu_logits, dim=1)
>>> target = F.softmax(tea_logits, dim=1)
>>> output = kl_loss(input, target)

KL 散度

衡量概率分布 \(Q\)（学生）与第二个参考概率分布 \(P\) （教师）有多大的不同。或者说，\(P\) 相对于 \(Q\) 的相对熵

\[ L(Q, P) = {\displaystyle D_{\text{KL}}(P\parallel Q)=\sum _{x\in {\mathcal {X}}}P(x)\ \log \left({\frac {\ P(x)\ }{Q(x)}}\right).} \]

其中，\(P\) 和 \(Q\) 作为概率分布可以用一个温度 \(T\) 来 平滑/尖锐 分布

知识蒸馏的变种

由于「知识」可以包含太多东西，所以只要跟模型相关的东西，都可以被认为是知识。

• 本身的权重 → 模型融合

• 中间层输出的特征 → 预训练后做下游的 Fine-tuning

• 最后一层输出的 logits → 经典知识蒸馏

• 模型输出的 logits 被解码成硬标签（类别信息、文本…） → “隐式”的知识蒸馏

知识蒸馏的 Q & A

Q：为什么是 KL 散度？

A：如果有更好、更简单的度量方式也可以替换，比如 Wasserstein metric

Q：为什么是大模型做教师？

A：

• 以压缩作为出发点，就是需要更好效果的模型来引导。

• 也可以是同等尺寸的模型做教师，只要能够在某项任务上表现足够好。关键词：自蒸馏

Q：预先训练一个教师模型有点麻烦

A：

• 消除掉这个过程。就类似于在线学习，关键词：在线蒸馏。

• 大模型通常收敛的会比小模型更快。（同时训练，并不是不训练）

• 教师模型通常会被“好心人”提供出来，做的工作不需要太多

Q：为什么用最后一层的 logits，中间层的行不行？

A：

• 可以用中间层，但会有些限制，需要引入额外的优化。关键词：特征蒸馏

• 架构可能不一样

• 选哪些层蒸馏哪些层。比如教师有20层，学生有10层，哪些层的输出作为拟合对象是不好确定的。

Q：其他 tricks

A：

• 温度 temperature，超参数。

• KL 的权重系数

• 蒸馏的计算方法

……

在 LLM 中的知识蒸馏

由于算力、数据等原因，开源模型往往弱于闭源模型。知识蒸馏是一种可能缩小这两者差距的手段。

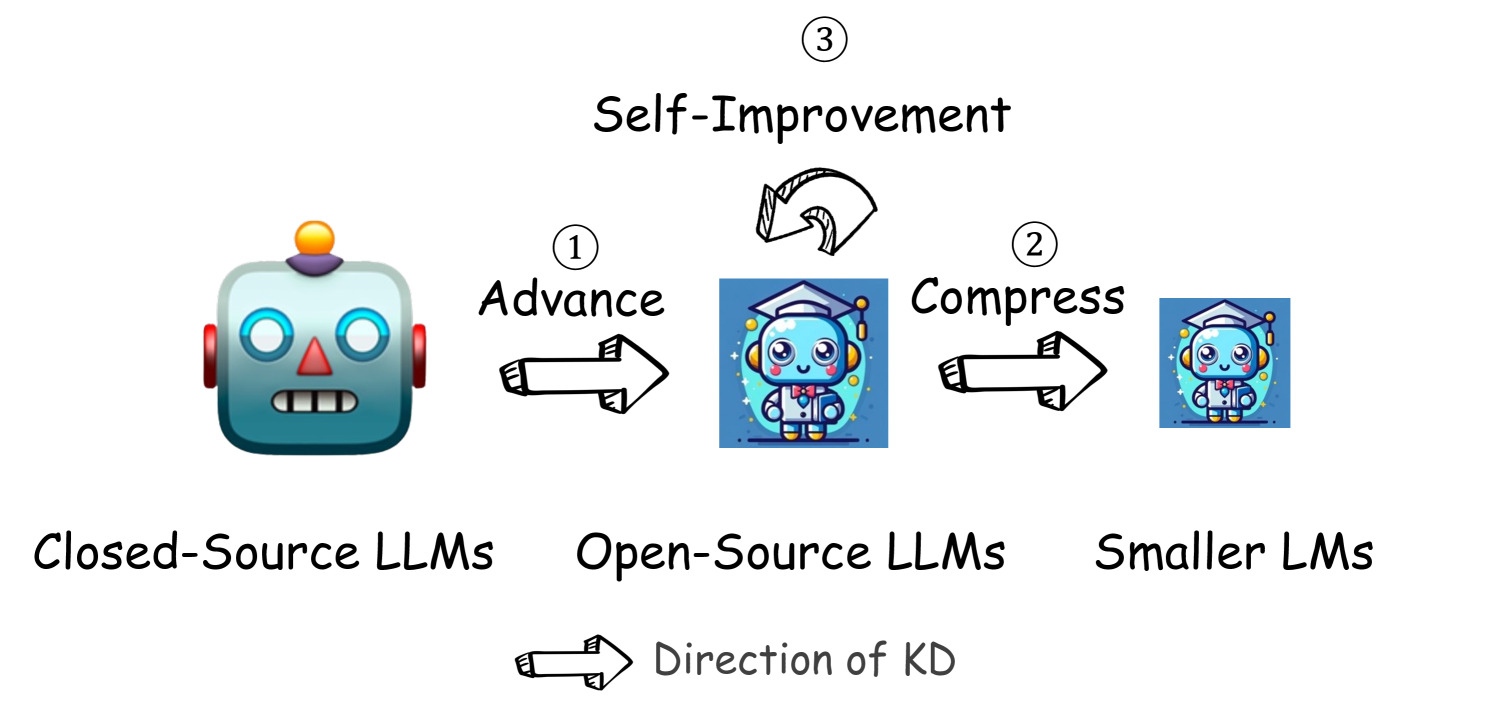
三种方法

• 针对特定领域，固定知识种子(凝练出若干特定的问题），用闭源模型生成更多的数据（隐式的知识蒸馏）。（PASS）

• 模型压缩（PASS）

• 自我提升（self-improvement）

  • SFT 模型生成数据标注后作为 DPO 的的训练数据，https://arxiv.org/abs/2305.18290

  • 用开源模型生成 Q & A 作为 SFT 训练数据， https://arxiv.org/abs/2406.08464

注：自我提升在蒸馏里面又被叫做自蒸馏

LLM SFT 中蒸馏的类别

LLM：在超多分类任务上进行训练的大尺寸模型。所以，相较于经典知识蒸馏，会有一些不同。

$p(x) $ 表示教师输出，$q(x) $ 表示学生输出

• Forward KD（经典蒸馏）: \[D_{\text{KL}}(P\parallel Q)=\sum_x p(x) \log [\frac{p(x)}{q(x)}]\]

• Reverse KD: \[D_{\text{KL}}(Q\parallel P)=\sum_x q(x) \log [\frac{q(x)}{p(x)}]\]

• JS Divergence: \[\frac{1}{2}(D_{\text{KL}}(P\parallel Q)+D_{\text{KL}}(Q\parallel P))\]

其他：对于模型中间层的输出进行对齐

Reverse KD

来源：https://agustinus.kristia.de/techblog/2016/12/21/forward-reverse-kl/

回顾 KL 损失

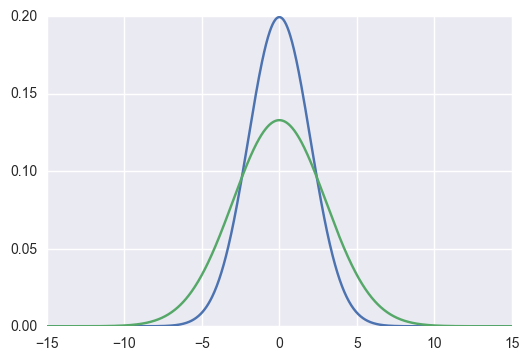
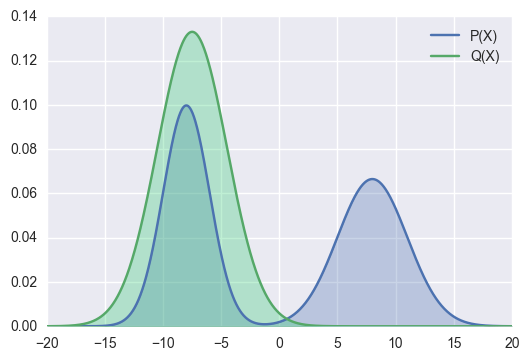
蓝线（教师）是 p(x)，绿线（学生）是 q(x)。KL 散度的就是计算 加权平均值。

\[ \sum_x p(x) \log [\frac{p(x)}{q(x)}] \]

那么，出现下面的情况时，KL 散度就会特别大（蓝线两个凸的区域）

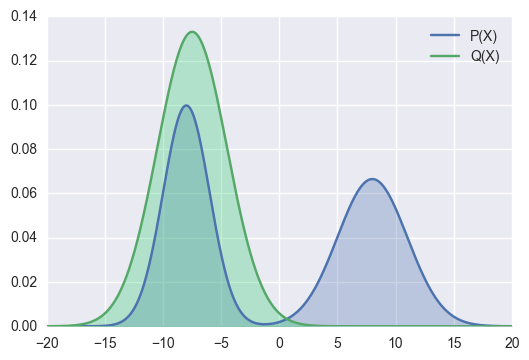
绿线拟合蓝线之后，会让绿线分布的更广泛（原来没有值的地方有值了）。

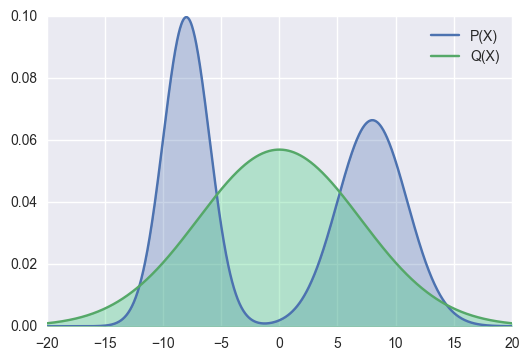
导致不应该有值的地方有值，对于某些输入x，有些类别概率应该为 0。

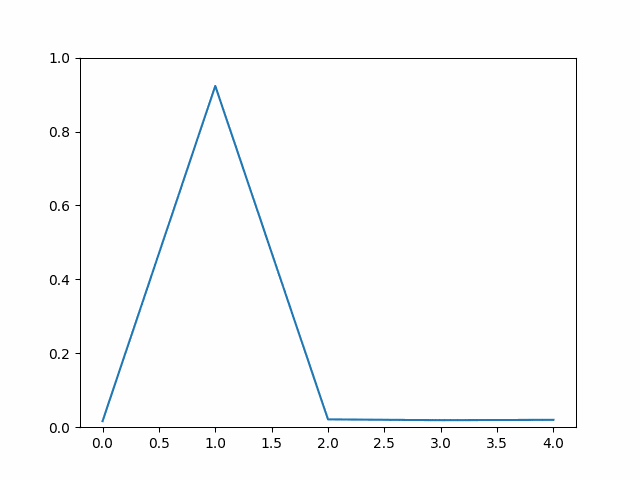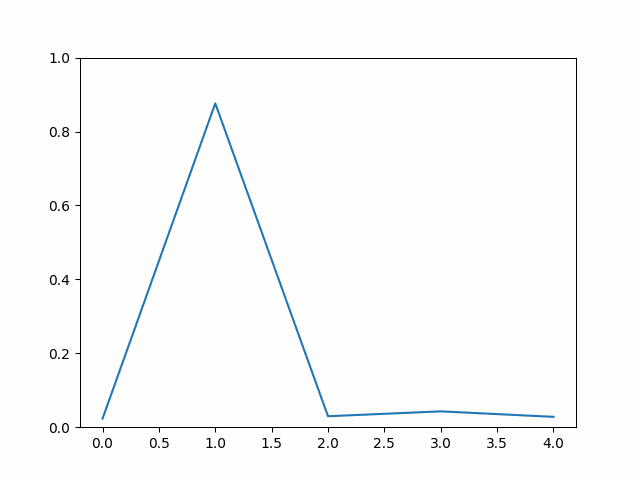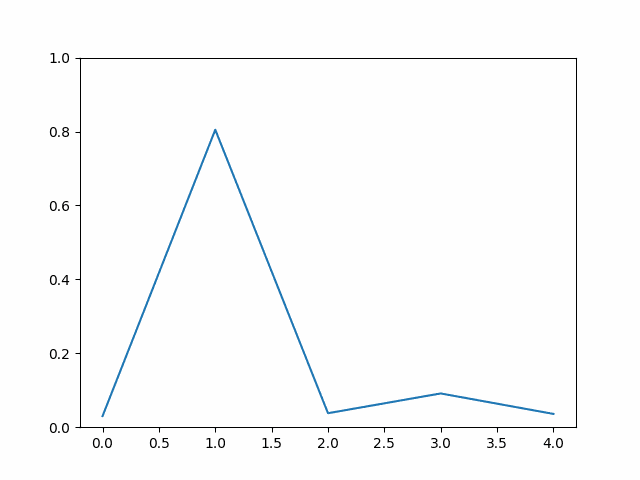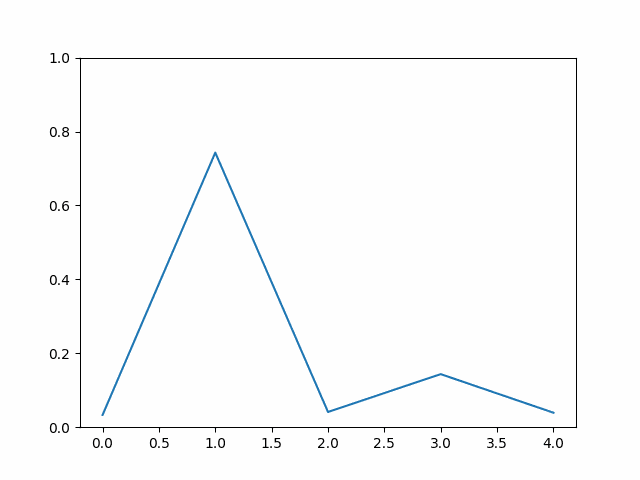
方法

Reverse KL 就是将 \(p\)、\(q\) 位置互换，

\[ \sum_x q(x) \log [\frac{q(x)}{p(x)}] \]

此时，再看刚刚这张图

\(q(x)\) 此时作为权重，会让绿线凸出来的地方更凹一些。但不会学习蓝色右侧凸的地方。

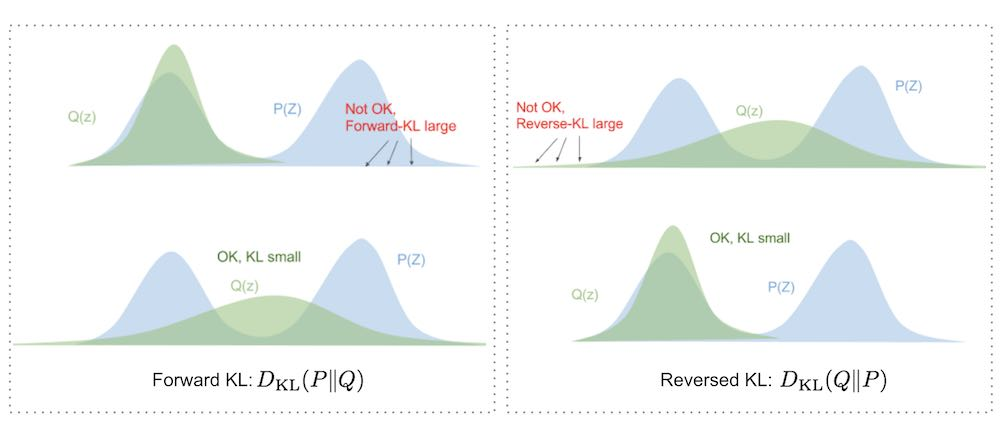
在 LLM 上，类别标签特别多，Forward KL 会使得各个 token id 更加“均匀”。

• 好：可以增加多样性

• 坏：学生可能会学到一些低质量的概率标签，从而导致生成幻觉和低质量文本

Reverse KL

• 好：避免了低质量标签

• 坏：过于相信学生的预测，如果学生的预测不是最优的（即绿色在蓝色的第二个凸出），会变差

小结

• 监督学习用 Forward KL → SFT 模型做教师

• 强化学习用 Reverse KL → DPO 训练模型做学生

Q：为什么 RL 用 Reverse KL？

A：强化学习在训练的时候，会“克隆”模型并更新原来的模型。如果用 Forward KL，在某些情况下 KL 值过高会导致模型不收敛。而 Reverse KL 一种更加稳妥的方式，能够保证 KL 散度足够小。且由于模型是克隆的，所以教师和学生的预测结果会比较相像，即不会出现学生预测在教师的次优上。

https://www.reddit.com/r/reinforcementlearning/comments/kcqbhv/hi_all_can_anyone_please_help_me_understand_how/

Summary

Jenson–Shannon (JS) Divergence

\[ \frac{1}{2}(D_{\text{KL}}(P\parallel Q)+D_{\text{KL}}(Q\parallel P)） \]

\[ \frac{1}{2}(\sum p(x) \log\frac{2p(x)}{p(x)+q(x)} + \sum q(x)\log\frac{2q(x)}{p(x)+q(x)}) \]

KL 是非对称的， JS 把两种分布的 KL 都算一遍，以此取得了对称的结果。

引入对称性带来的缺点：

• 计算复杂度高：计算了两次 KL Divergence

• 数值稳定性差：如果 P 和 Q 的概率分布差异较大，可能会出现零或非常小的概率值。比如 p(x) 某项为 0

且非对称性有时候不是一种缺点，是一个 feature。

非对称性带来了什么：保留「预测分布」到「目标分布」的方向信息

• 在真实分布 P 中常见的事件，如果在预测分布 Q 中的概率较低。有助于模型优化。

注：还有一个 TVD 方法，类似于 JS 度量，但它用 L1 范数代替了 KL

Forward KD（经典蒸馏）

Baby Llama：https://arxiv.org/abs/2308.02019

Less is More：https://arxiv.org/abs/2210.01351 （Bert）

分两阶段蒸馏

• Stage 1: 蒸馏训练最后一层

• Stage 2: 蒸馏训练中间层，每层有一个 loss

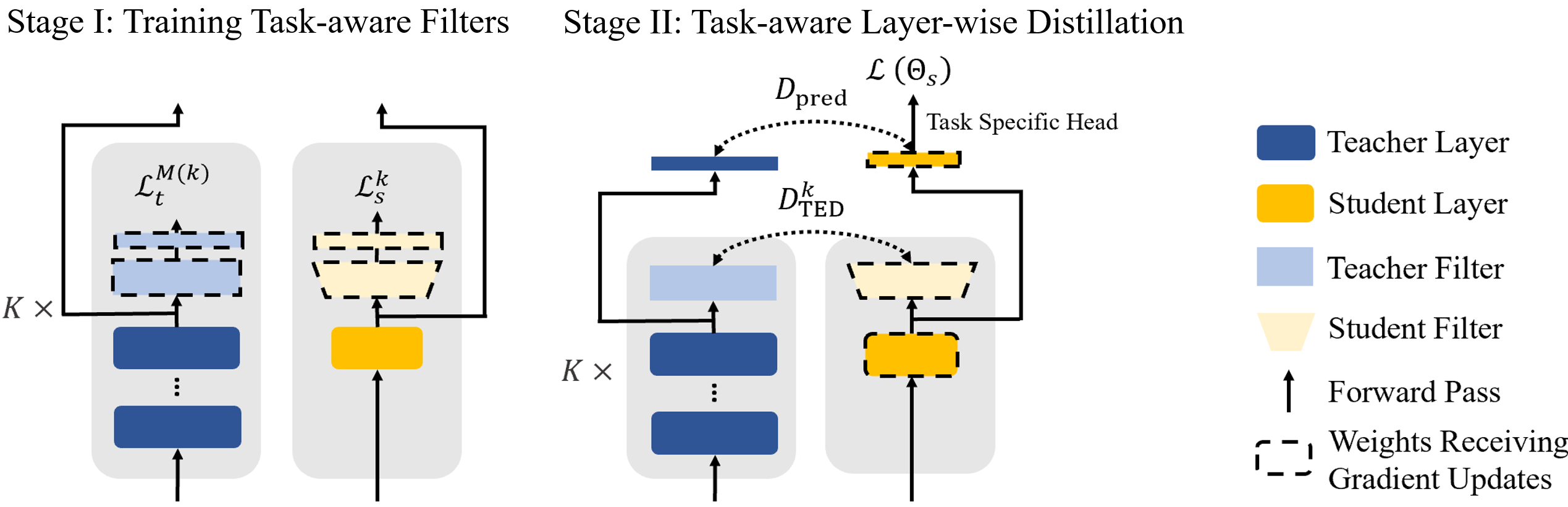
Reverse KD

论文

论文代码

动机

void regions (空洞区域)

where 𝑝′ can be real data distribution (word-level KD) or teacher distribution 𝑝 (sequence-level KD). Though widely used, KL[𝑝||𝑞𝜃] has been shown to overestimate the void regions of 𝑝 in language generation tasks when 𝑞𝜃 is insufficiently expressive to cover all the modes of 𝑝′

. KD for LLMs fits the case because LLMs perform various tasks in a generative manner, such that the low-capacity student models cannot perfectly imitate the complex language generation distribution of the teacher models or humans.

• 模式覆盖问题：真实数据（或教师模型）的分布 ( p ) 可能包含很多复杂和多样的语言模式，而学生模型 ( $q_{} $ ) 受限于模型复杂度或训练数据的局限，可能无法涵盖所有模式。

• 生成质量问题：这会使得训练过程中更多关注这些难以覆盖的模式，导致学生模型无法有效提高在常见模式上的生成质量。

方法

tea_probs = F.softmax(tea_logits, dim=-1, dtype=torch.float32)
stu_probs = F.log_softmax(logits, dim=-1, dtype=torch.float32)

# 标准 KD
kd_loss = (tea_probs*(tea_probs.log()-stu_probs)).sum()

# 化简
kd_loss = (tea_probs*std_probs).sum()

# 低方差估计，a low-variance estimation KD
# http://joschu.net/blog/kl-approx.html
log_ratio = (stu_probs - tea_probs.log())
kd_loss = log_ratio.float().exp() - 1 - log_ratio

Approximating KL Divergence

标准的 KD

\[ KL[q, p] = \sum_x q(x) \log [\frac{q(x)}{p(x)}] = E_{ x \sim q}[\log \frac{q(x)}{p(x)} ] \]

由于精确计算需要花费更多的内存，所以期望对齐进行估计，从而减少计算量。

Step 1

一种直接的思路是直接去掉最外面的 \(q(x)\)，演变成了

\[ -\log\frac{p(x)}{q(x)} \]

因为舍去了系数，它会使得方差变高

Step 2

加上平方，降低方差

\[ \frac{1}{2}(\log\frac{p(x)}{q(x)})^2 \]

Step 3

依赖数学背景公式

\[ \log(x)\leq x-1 \]

但保证该公式 \(>= 0\) 时，就有

\[ (x-1) - \log(x) \geq 0 \]

把这里 \(x\) 换成 \(p(x) / q(x)\) 就得到了代码的计算方法

Optimization with Policy Gradient

优化公式

\[\theta=\arg\min\limits_{\theta}\mathcal{L}(\theta)=\arg\min\limits_{\theta}\mathrm{KL}[q_{\theta}||p]=\arg\operatorname*{min}_{\theta}\left[-\operatorname*{lim}_{x\sim p_{\infty},y\sim q_{\theta}}\log{\frac{p(y|x)}{q_{\theta}(y|x)}}\right]\]

Policy Gradient Theore 求导

\[\nabla{\mathcal{L}}(\theta)=-\operatorname*{\mathbb{E}}_{\mathbf{x}\sim p_{\mathbf{x}},y\sim q_{\theta}(\,\cdot\,|\mathbf{x})}\sum_{t=1}^T(R_{t}-1)\nabla\log q_{\theta}(y_{t}|\mathbf{y}_{<t},\mathbf{x}),\]

其中，$R_t $ 是每一步生成的累积，衡量每一步的生成质量

\[R_{t}=\sum_{t^{\prime}=t}^{T}\log\,\frac{p(y_{t^{\prime}}|y_{<t^{\prime}},\mathbf{x})}{q_{\theta}(y_{t^{\prime}}|y_{<t^{\prime}},\mathbf{x})}\]

三个优化

优化1：Single-Step Decomposition

单步生成的质量都很重要，所以把单步生成和累积生成拆开，并直接计算单步生成的梯度

$$ \[\begin{array}{c} \nabla \mathcal{L}(\theta) = \mathbb{E}_{x\sim p_{x},y\sim q_{\theta}(\,\cdot\,|x)}\left[-\sum\limits_{t=1}^{T}\nabla\mathbb{E}_{p_{t}\sim q_{\theta}(t)}[r_t]\right]+{\mathbb{E}}_{x\sim p_{x},y\sim q_{\theta}(\,\cdot\,|x)}\left[-\sum\limits_{t=1}^{T}R_{t+1}\nabla\log q_{\theta}(y_{t}|\bm{y}_{<t},\bm{x})\right]\\ =(\nabla \mathcal{L})_\mathrm{single}+(\nabla \mathcal{L})_{\mathrm{Long}} \end{array}\]

$$

优化2：Teacher-Mixed Sampling

教师生成的句子可能会重复，所以用教师和学生的混合分布来代替原有的教师分布 (px)，并且用 $$ 来控制强度。

\[\tilde{p}(y_{t}\,|\,y_{<\,t},x)=\alpha\cdot p(y_{t}\,|\,y_{<\,t},x)+(1-\alpha)\cdot q_{\theta}(y_{t}\,|\,y_{<\,t},x),\]

即，

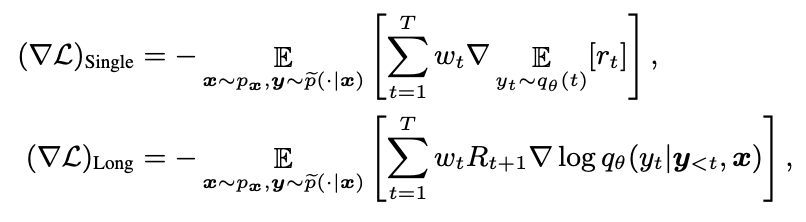
优化3：Length Normalization

模型会为了更低的损失，容易“偷懒”生成短文本。为了消除长度影响，加入长短文本的归一化操作

\[R_{t+1}^{\mathrm{Norm}}=\frac{1}{T-t-1}\sum_{t^{\prime}=t+1}^{T}\log\frac{p(y_{t^{\prime}}|y_{<t^{\prime}},\mathbf{x})}{q_{\theta}(y_{t^{\prime}}|y_{<t^{\prime}},\mathbf{x})}.\]

综上，最后的公式为

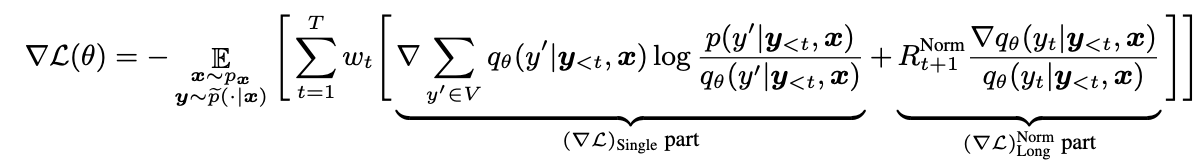
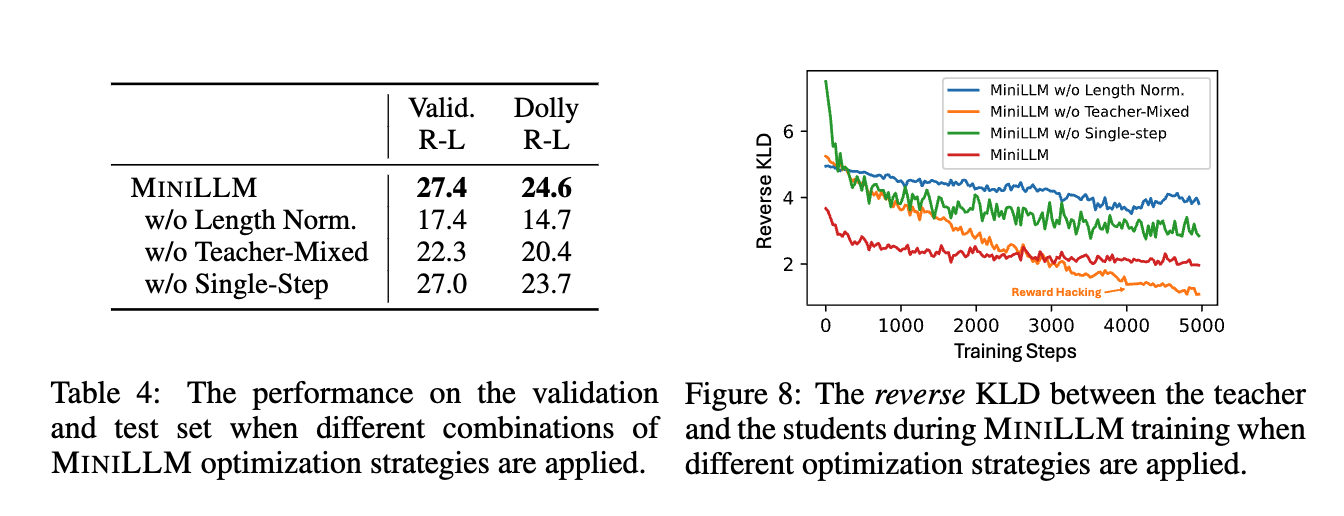
结果

• SFT w/o KD：标准 SFT

• KD： 标准 SFT 加入 KD 损失，又称为 Word-Level KD

• SeqKD：句子级别的KD，在教师模型生成的数据上进行微调

• MINILLM：提出的方法，reverse KD + PPO + 若干 tricks

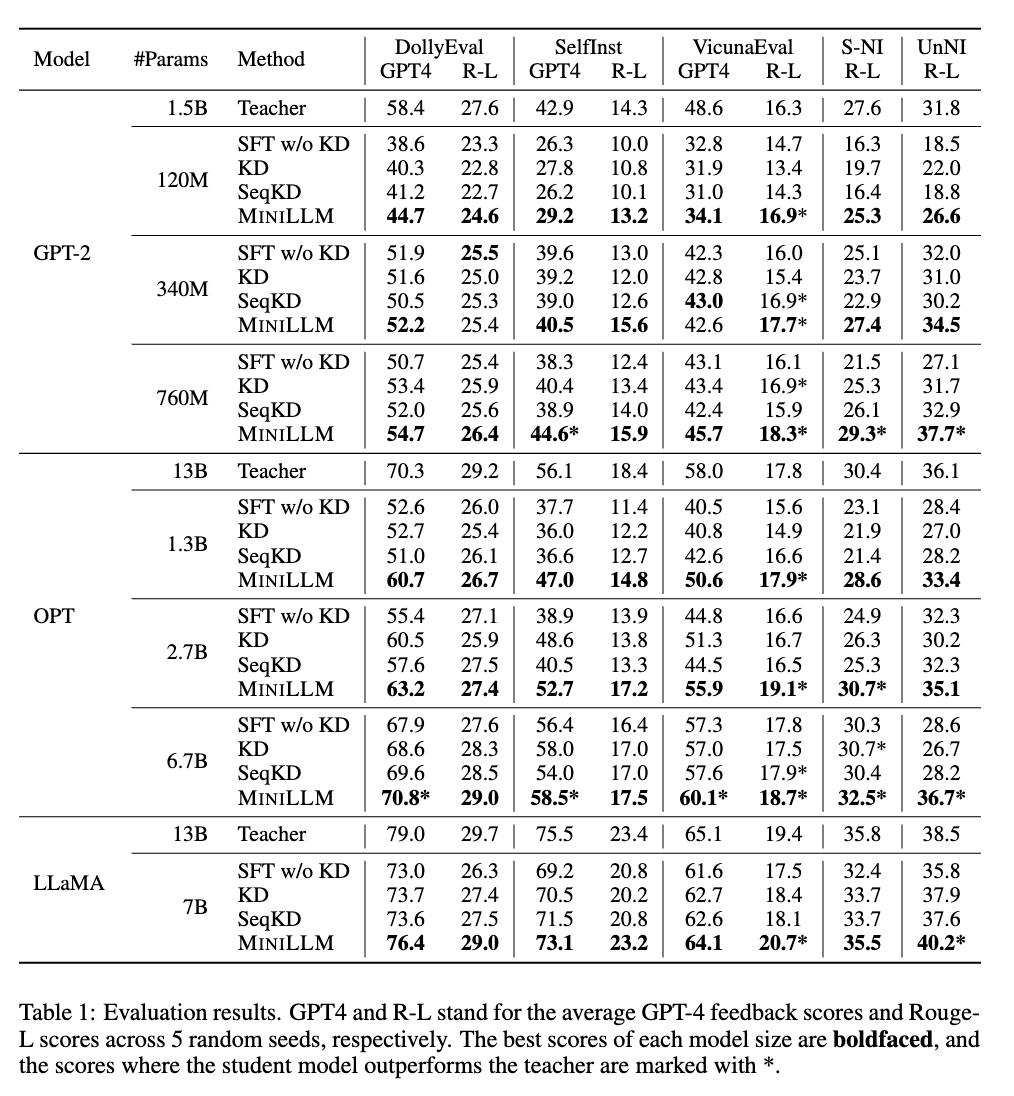
消融实验

解耦知识蒸馏

论文

背景知识

论文

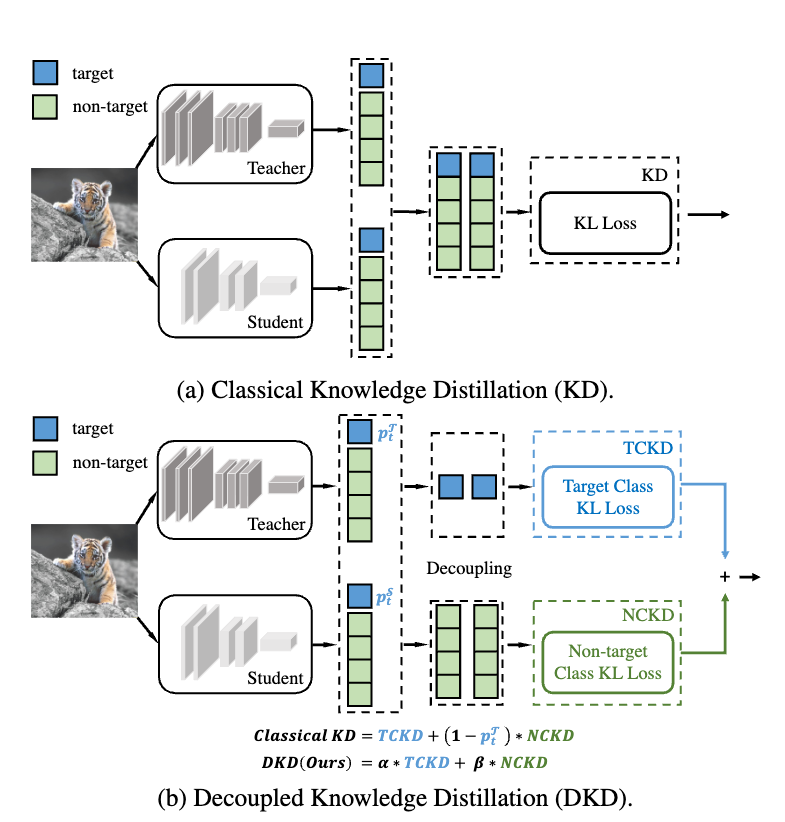
把 KD 拆成了两个部分，DKD+TKD。其中，

• TKD 指的是 ground truth 对应的 logits （TCKD）

• DKD 指的是非 ground truth 对应的 logits（NCKD）

>>> import torch.nn.functional as F
>>> kl_loss = nn.KLDivLoss(reduction="batchmean")
>>> stu_logits = torch.randn(3, 5, requires_grad=True)
>>> tea_logits = torch.randn(3, 5)

经典 KD

>>> input = F.log_softmax(stu_logits, dim=1)
>>> target = F.softmax(tea_logits, dim=1)
>>> loss = kl_loss(input, target)

DKD + TKD

>>> dkd_tea = F.softmax(tea_logits - 1000 * gt_mask, dim=1)
>>> dkd_stu = F.log_softmax(stu_logits - 1000 * gt_mask, dim=1)
>>> dkd_loss = kl_loss(dkd_stu, dkd_tea)

>>> tea_probs = F.softmax(tea_logits)
>>> stu_probs = F.softmax(stu_logits)
# 假设 tea_probs = [0.4, 0.3, 0.3], stu_probs = [0.2, 0.6, 0.2]
# target 为第 0 个位置
# tkd_loss  为 [0.4, 0.6] 和 [0.2, 0.8] 它们的 kl 散度
>>> output = w1*dkd_loss + w2*tkd_loss

TKD：样本的“难度”信息

transfers the knowledge concerning the “difficulty” of training samples.

DKD：样本的“暗知识”

is the prominent reason why logit distillation works but is greatly suppressed.

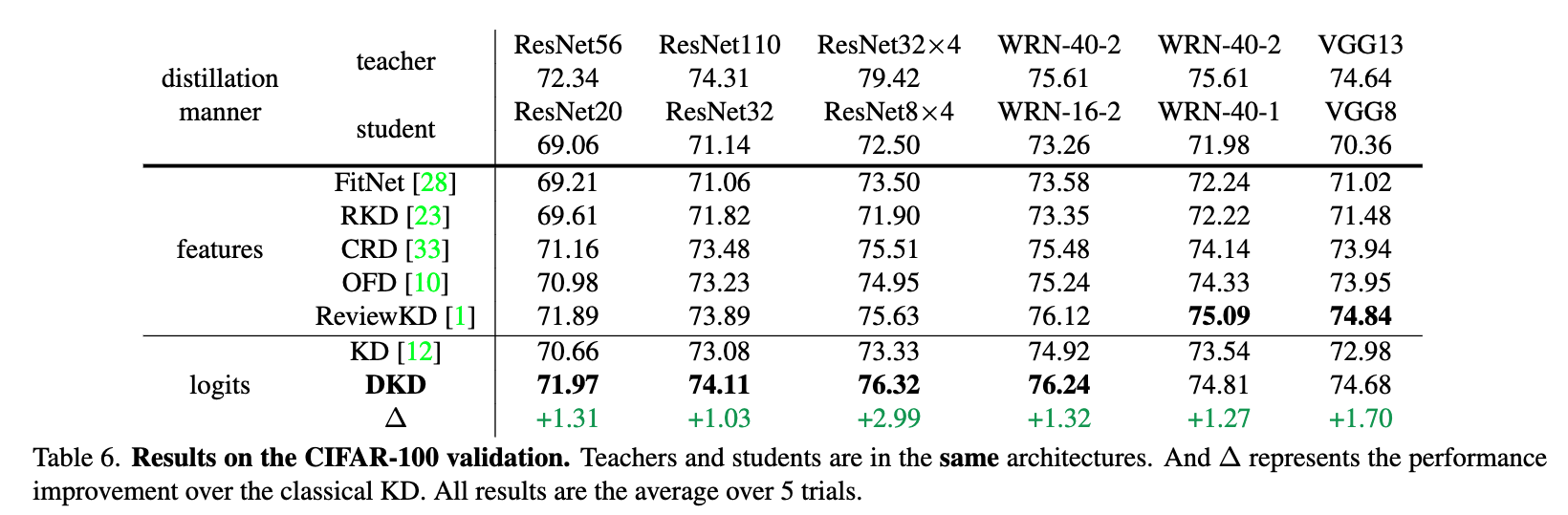
结果

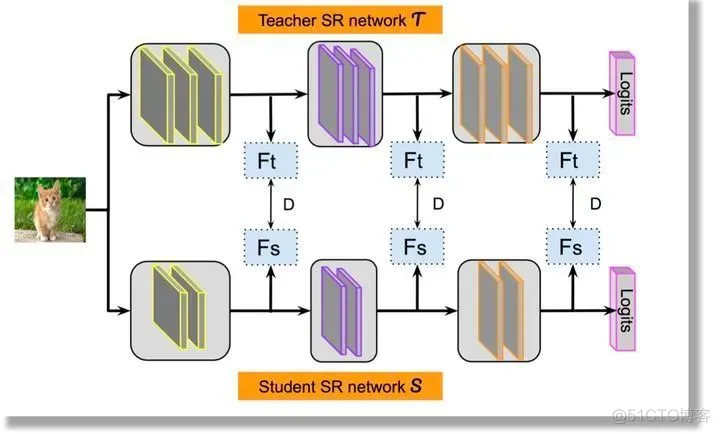
特征蒸馏：在模型中间层增加度量的损失函数

代码

发现

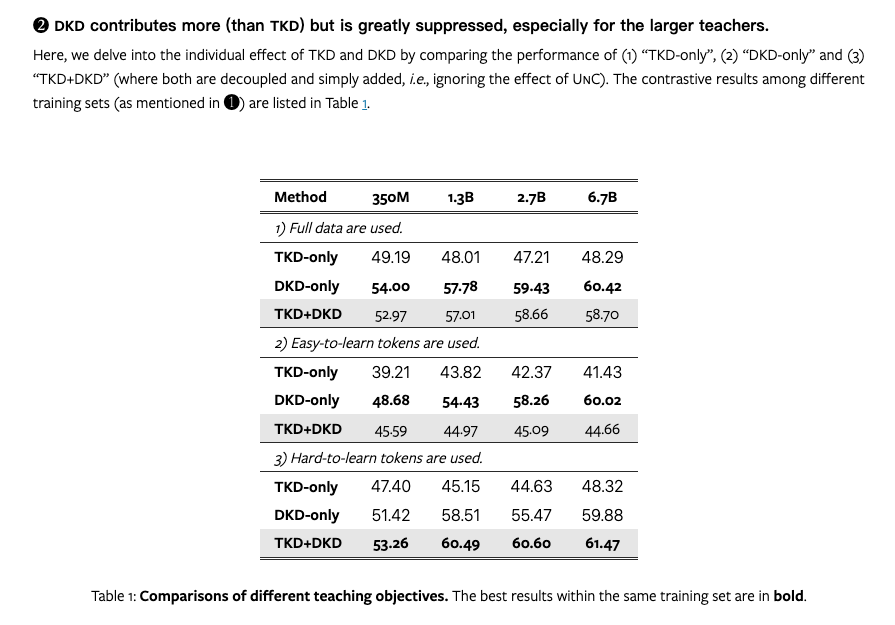
• 大部分情况下，非 ground truth （DKD）蒸馏效果会优于其他效果

• 小部分情况（难学的情况），加上 TKD 会更好。

方法

hard to learn 的定义

\[ p_{g_{t}}^{t}=\frac{\exp(z_{g_{t}}^{t})}{\sum_{j=1}^{C}\exp(z_{j}^{t})},p_{\backslash g_{t}}^{t}=\frac{\sum_{k=1,k\neq g_{t}}^{C}\exp(z_{k}^{t})}{\sum_{j=1}^{C}\exp(z_{j}^{t})} \]

对于每个要预测的 token，教师模型会输出一个 logits，gt 表示 ground truth 的 token，而 表示非 ground truth 的 token。

补充，

• \([0.1,0.9]\) 好学

• \([0.5,0.5]\) 不好学

所以，这里是对 logits 取 softmax 后的结果（概率），UNC 为 非 ground truth token 的 概率值之和。其越大则表示这个越难学。

通过 UNC 这个指标变成成 TKD 的系数，自适应的训练。

结果

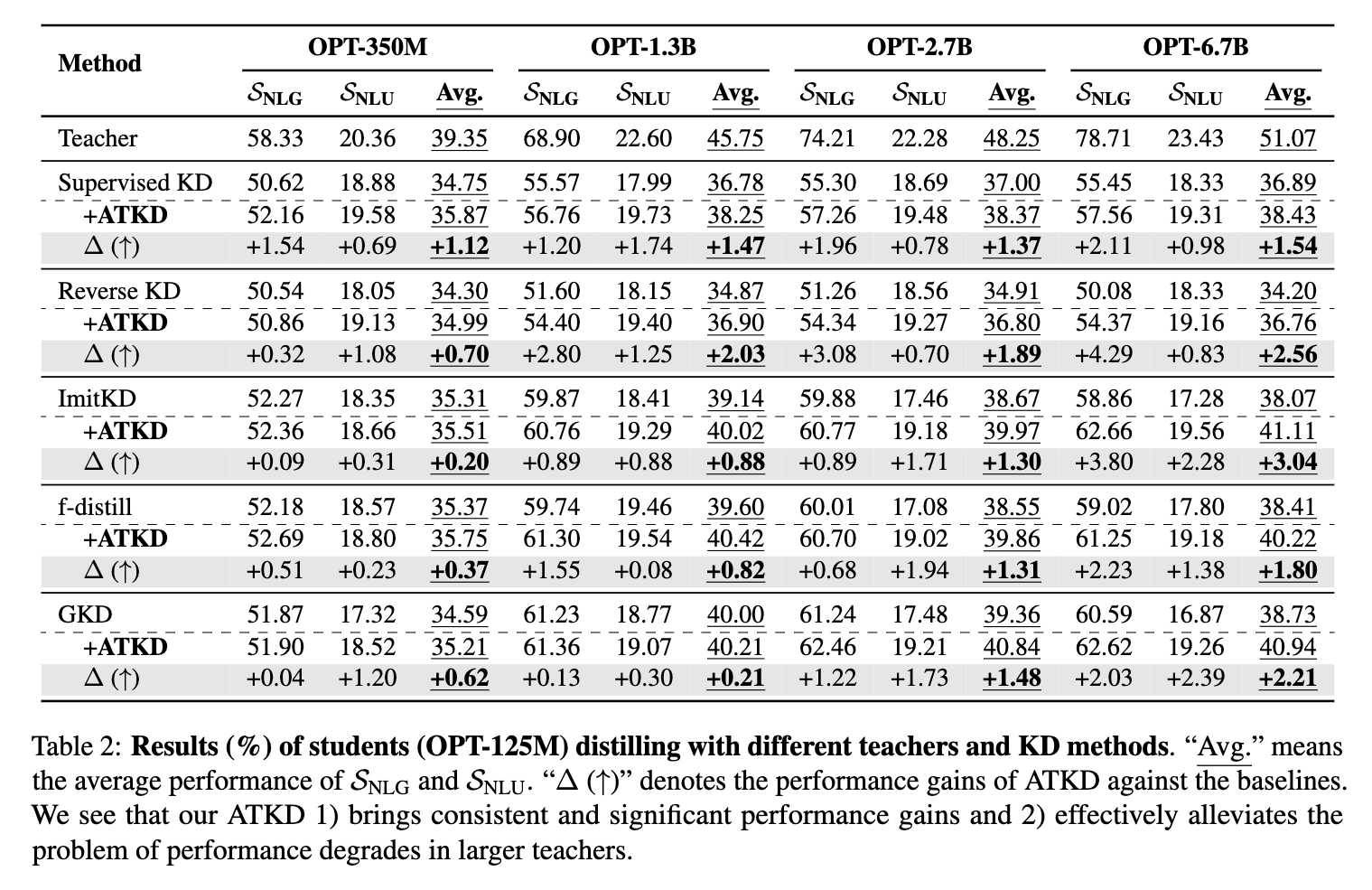
写在最后

「你好，」后面可以接「世界」，可以接「北京」。

在训练的时候，有两条样本「你好，世界」和「你好，北京」。这个时候，对于任意一条样本，「世界」和「北京」的 one-shot 编码是 [0, 1, 0] 和 [0, 0, 1] 。

两个不确定：

• 无法控制模型最终学到的概率分布是什么样的

• 不知道最佳分布是什么

知识蒸馏：

• 可以更容易控制学生模型学习哪种分布

• 教师模型会输出一种更好的分布