介绍 vLLM 的 PageAttention 加速
博客
论文
代码
文中 GIF 图来源于 vLLM 博客
动机
定义
当前模型生成的机理是，给定 Prompt，输出
Completion。模型在生成时有一个参数
MAX_SEQ_LEN，以控制模型最大能处理的长度（Prompt + Completion）。
问题
经典的框架在生成时，会提前申请 MAX_SEQ_LEN 的长度。然而，最后生成的
Prompt + Completion 的长度往往可能是小于 MAX_SEQ_LEN
的。从而导致有很大显存的浪费，且生成之后，该部分显存又将丢弃，从而导致操作的浪费。
小结
传统方法在生成时，会有申请/丢弃显存的 IO
浪费，模型在处理时会有冗余显存始终未被利用到，导致模型能处理的
Prompt 低于理想情况，计算浪费。
怎么做
冗余的部分来自于，attention
计算中的空间。因此，借鉴操作系统中虚拟内存和分页的经典思想，将空间打碎，从而实现更高效的空间利用。
翻译后的原句：PagedAttention
允许在非连续的内存空间中存储连续的键和值。具体来说，PagedAttention
将每个序列的 KV
缓存划分为块，每个块包含固定数量的标记的键和值。在注意力计算过程中，PagedAttention
内核有效地识别并获取这些块。
kv cache 空间计算：
\(2 \times 5120 \times 40 \times 2 \times
2048 / (1024 ** 3)\) GB = 1.5625 GB
(k+v) \(\times\) hidden_size \(\times\) num_layers \(\times\) FP16 bytes \(\times\) tokens_num
对于 13B 模型 2048 的 seq_len 而言，需要申请 1.56 GB 的显存。而如果
Prompt + Completion 的长度只有 1024，那么将浪费 0.78 G
的显存（在没有其他 kv 优化的情况下）
如下图所示，block 存储了所有可能的 token。在生成时，模型从 block
中进行计算。
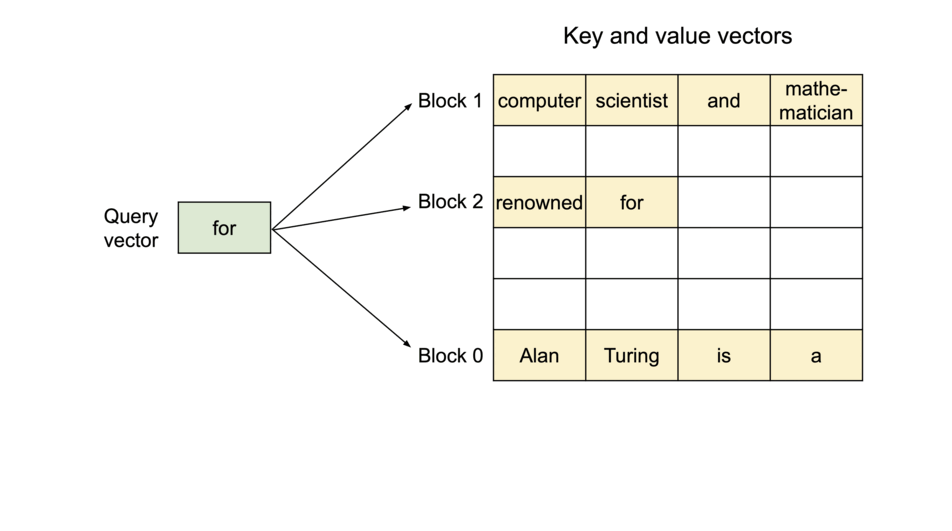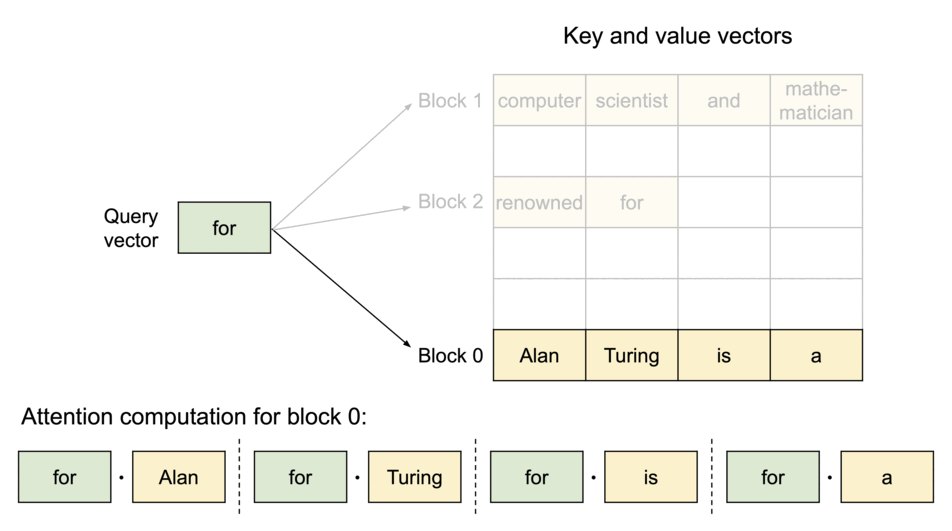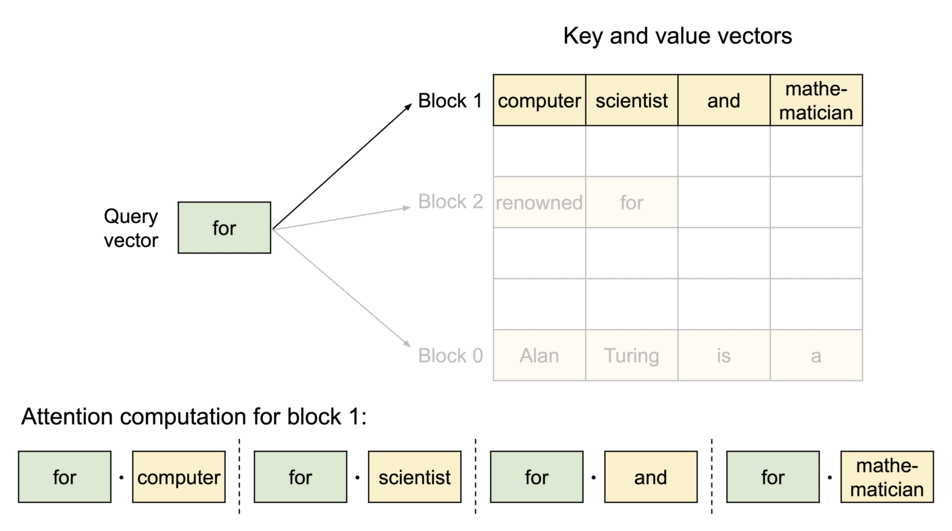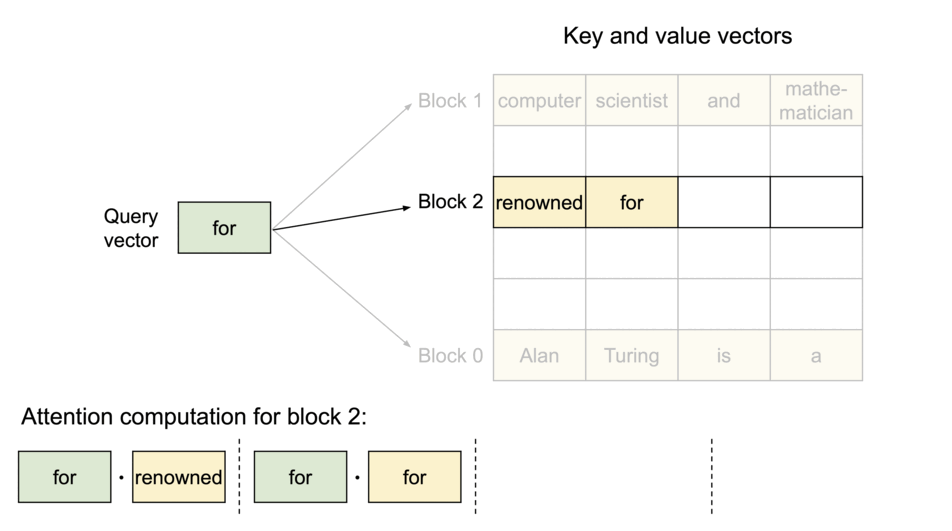
Attention 计算公式
\[a _ { i j } = \frac { \operatorname {
exp } ( q _ { i } ^ { T } k _ { j } / \sqrt { d } ) } { \sum _ { t = 1 }
^ { i } \operatorname { exp } ( q _ { i } ^ { T } k _ { t } / \sqrt { d
} ) } , o _ { i } = \sum _ { j = 1 } ^ { i } a _ { i j } v _ { j
}\]
PageAttention 计算公式
\[A _ { i j } = \frac { \operatorname {
exp } ( q _ { i } ^ { T } K _ { j } / \sqrt { d } ) } { \sum _ { t = 1 }
^ { \lceil i / B \rceil } \operatorname { exp } ( q _ { i } ^ { T } K _
{ t } 1 / \sqrt { d } ) } , o _ { i } = \sum _ { j = 1 } ^ { \lceil i /
B \rceil } V _ { j } A _ { i j } ^ { T }\]
对于 query (q)，不需要改变，而 k 和 v 转变为 block
的形式。计算步骤如下
- 提取对应的 block
- 计算 q 和 block 中每个元素的结果，汇总会注意力分数 A
- 注意力分数 A 与 block 中 V 相乘，得到输出
细节实现
如下图所示，kv cache 分了 logical block 和 physical
block，前者和后者内容是一样的，通过 Block table
找到在显存中的实际位置。
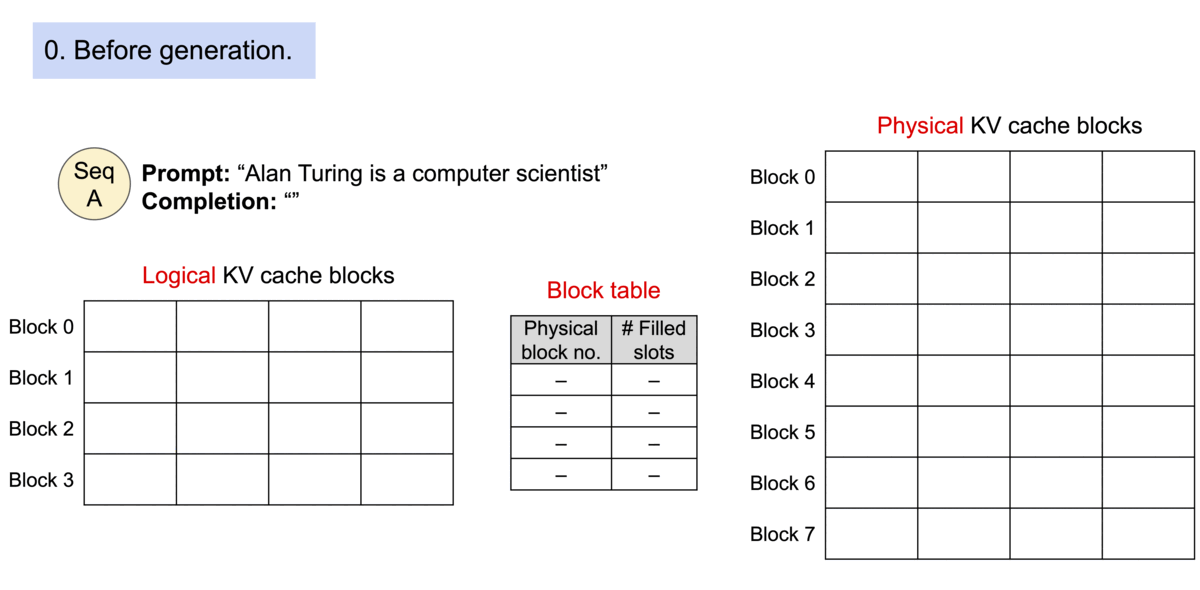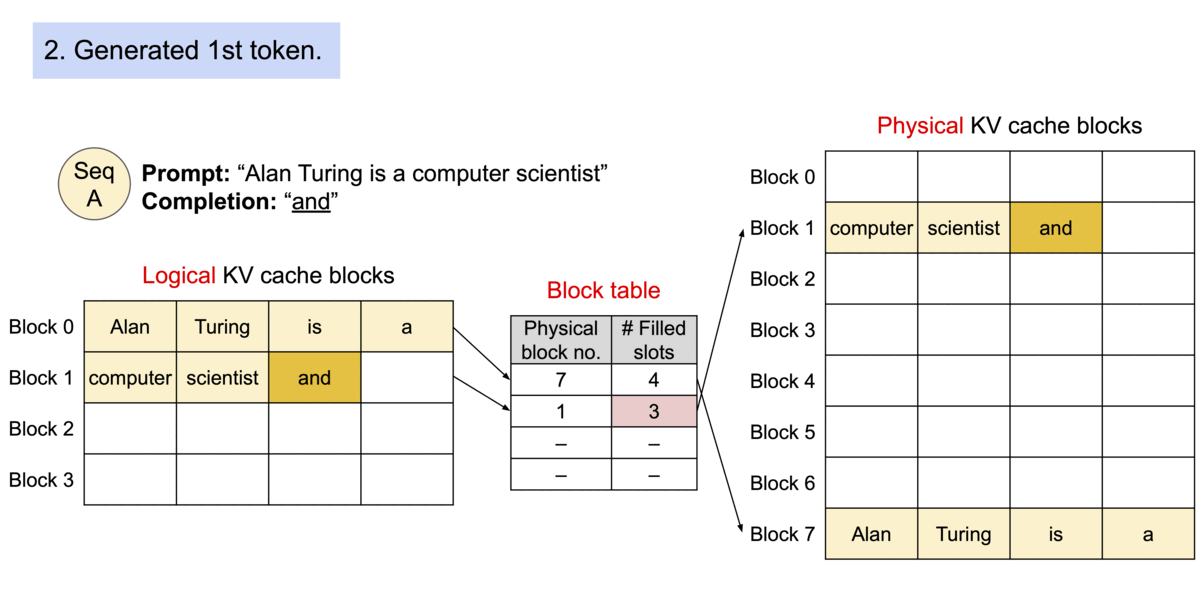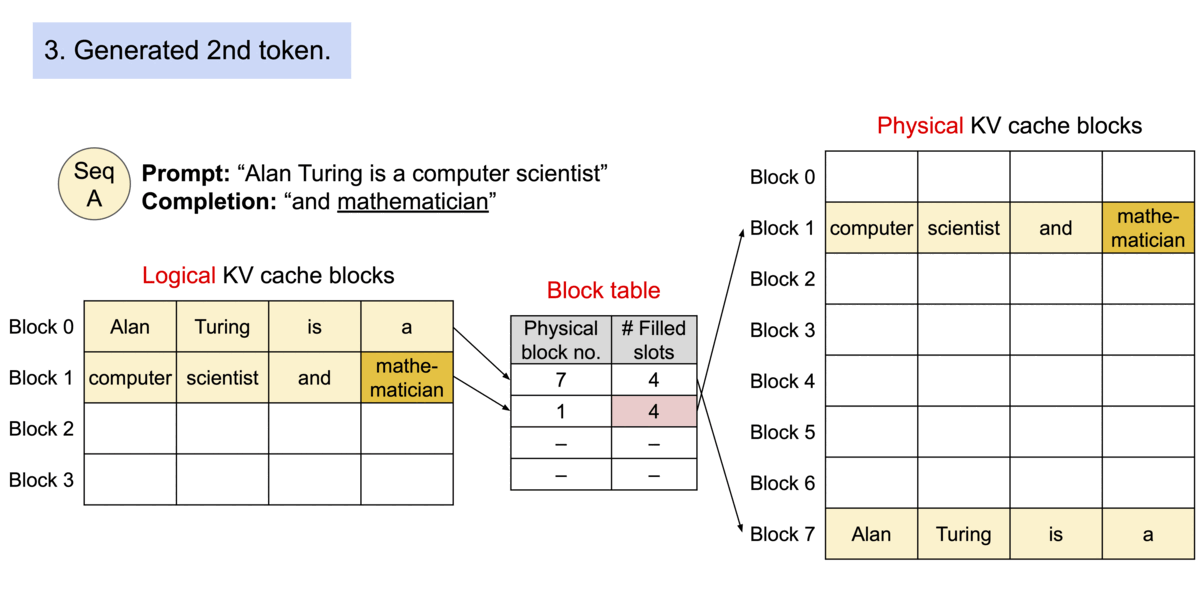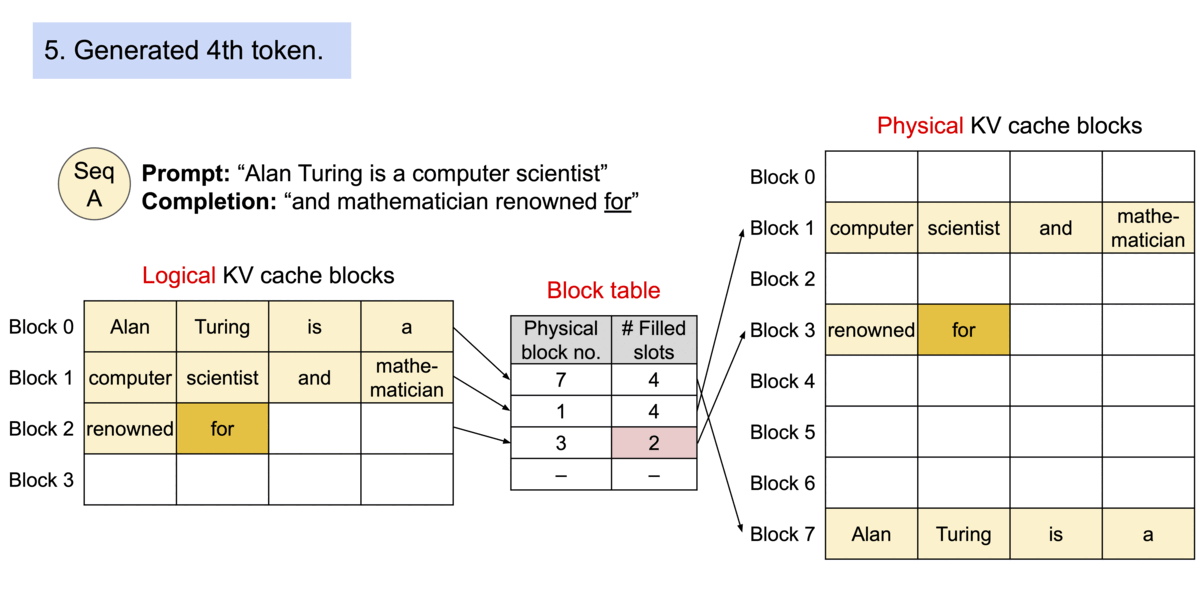
而如果是多个句子同时请求，那么在显存足够的情况下，多个句子会同时处理。如下所示，每个句子有自己的
logical block，共同映射到 physical block 中。（多个句子会一起计算）
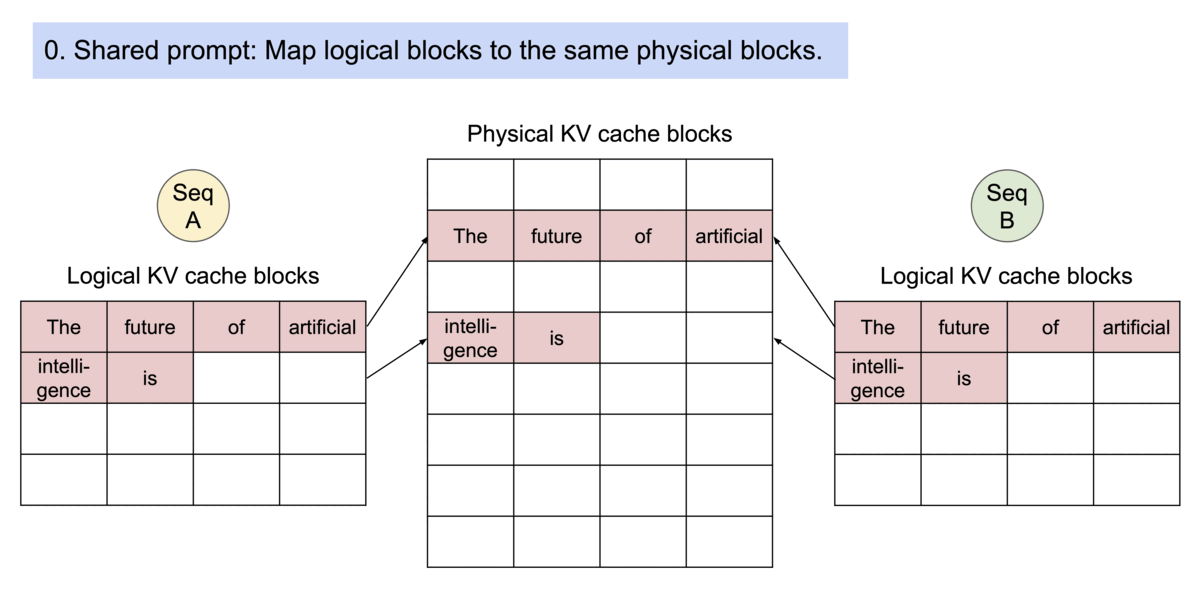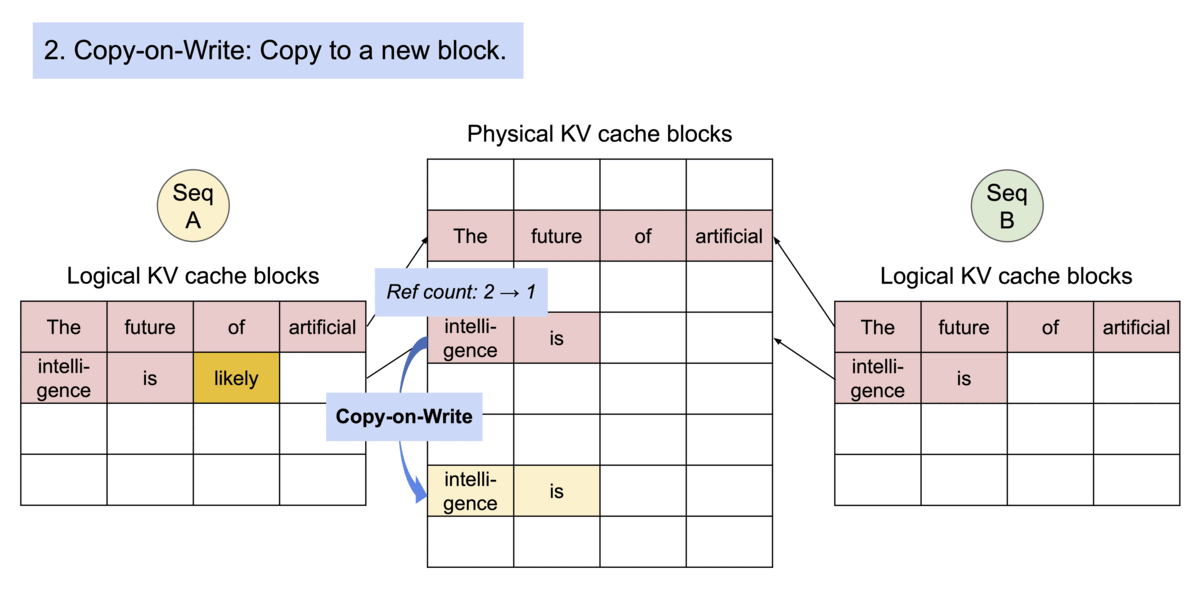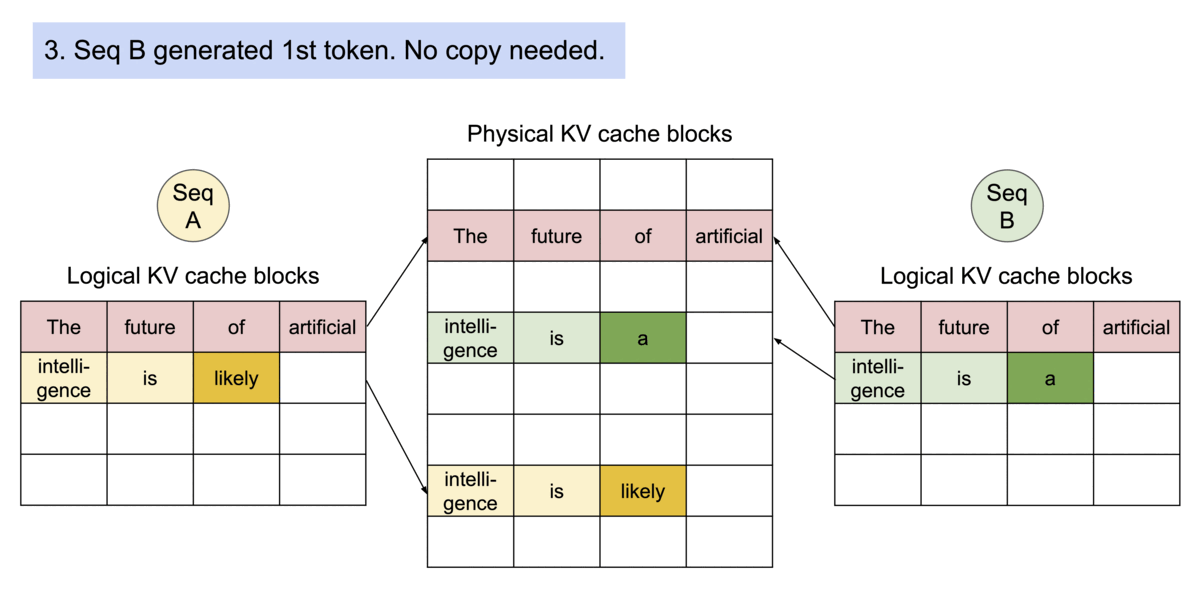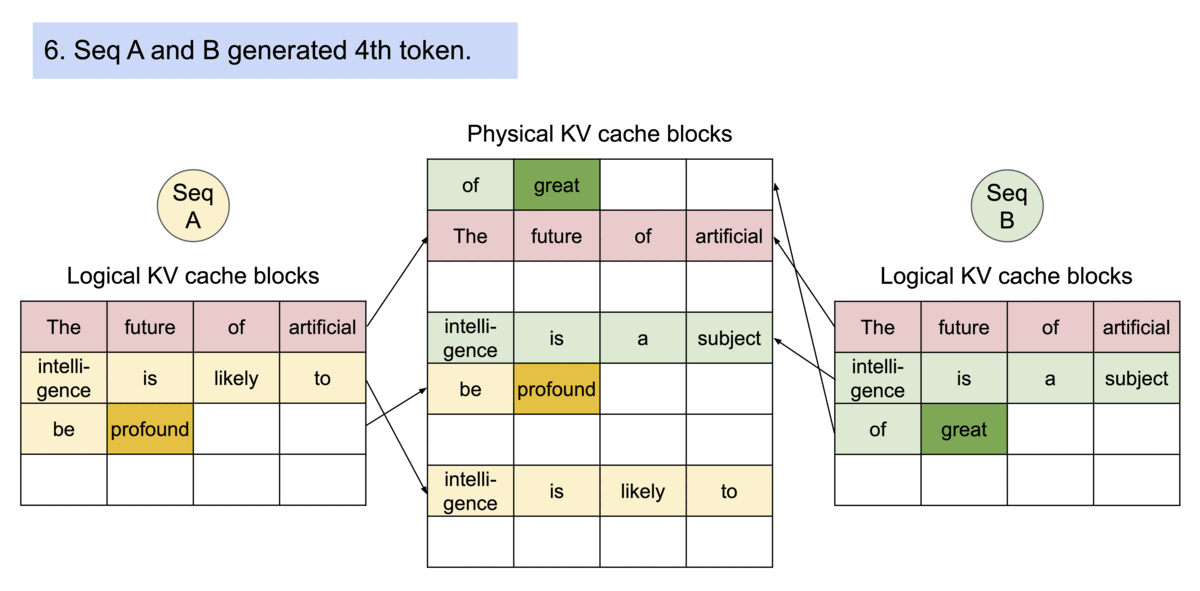
代码实现
调度是通过 Python
实现的，这一部分逻辑有些杂乱，之后再看。这里主要关注 PageAttention
的计算，核心的代码如下
背景知识
#pragma unroll
控制了其紧跟着的下一个循环的展开（为了加速使用，下面将删除对应行）
__syncthreads();
是CUDA并行编程中的一个同步指令，用于确保在同一个线程块内的所有线程都到达此指令位置后才能继续执行后面的代码，意味着在这个函数之前的所有操作都已经完成，buffer或者内存的数据已经得到同步更新。（下面将删除对应行）
__shfl_xor_sync：进行数据交换和归约操作
__shfl_sync：广播操作
WARP_SIZE：在CUDA编程中，WARP_SIZE通常指的是一个warp中的线程数。warp是CUDA硬件的一个基本执行单元，每个warp包含了一定数量的线程，这些线程会同时执行相同的指令。WARP_SIZE 通常定义为32，这意味着每个warp包含32个线程。
逐步拆建，首先，确定这段函数在干啥。它代替了 Python
的以下计算，简单来说有两个矩阵乘法，以及一个 softmax
操作。涉及到的变量有 q、k、v。（忽略 mask）
1
2
3
| score = torch.matmul(q, k.transpose(2, 3)) / math.sqrt(self.head_dim)
score = nn.functional.softmax(score, dim=-1, dtype=torch.float32).to(q.dtype)
out = torch.matmul(score, v)
|
之后，再捋一捋变量的数据结构，从下面的代码开始，假设 q、k、v 的
num_head 和 head_size 是相同的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
def attention(q, k, v, mask):
return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v
def func(x, kvcache):
x = mlp(x, **c_attn)
qkv = np.split(x, 3, axis=-1)
if kvcache:
new_q, new_k, new_v = qkv
old_k, old_v = kvcache
k = np.vstack([old_k, new_k])
v = np.vstack([old_v, new_v])
qkv = [new_q, k, v]
current_cache = [qkv[1], qkv[2]]
qkv_heads = list(map(lambda x: np.split(x, n_head, axis=-1), qkv))
if kvcache:
causal_mask = np.zeros((1, k.shape[0]))
else:
causal_mask = (1 - np.tri(x.shape[0])) * -1e10
out_heads = [attention(q, k, v, causal_mask) for q, k, v in zip(*qkv_heads)]
|
而在 PageAttention 中，k 和 v 分别用 block
再拆了一遍，所以需要多两个维度 num_blocks 以及
block_size。并且，为了实现连续 Batch，n_seq 将会被拼成一个 seq
处理。所以最后结构如下：
- q: [n_seq, n_head, head_size]
- k: [num_blocks, n_head, head_size, block_size]
- v: [num_blocks, n_head, head_size, block_size]
这里的 head_size = n_embd/n_head，且调换了一些维度。
而对于输出 out: [n_seq, n_head, head_size]
接下来看关键实现。假设有两个请求，seq1 = [1, 2, 3], seq2 = [1, 3, 4,
5]。vLLM 会将其拼成一个 seq = [1,2,3,1,3,4,5]
取 q
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
const scalar_t* q_ptr = q + seq_idx * q_stride + head_idx * HEAD_SIZE;
__shared__ Q_vec q_vecs[THREAD_GROUP_SIZE][NUM_VECS_PER_THREAD];
for (int i = thread_group_idx; i < NUM_VECS_PER_THREAD; i += NUM_THREAD_GROUPS) {
const int vec_idx = thread_group_offset + i * THREAD_GROUP_SIZE;
q_vecs[thread_group_offset][i] = *reinterpret_cast<const Q_vec*>(q_ptr + vec_idx * VEC_SIZE);
}
|
取 k 和 第一个矩阵乘法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
#define WARP_SIZE 32
float qk_max = -FLT_MAX;
const int* block_table = block_tables + seq_idx * max_num_blocks_per_seq;
for (int block_idx = start_block_idx + warp_idx; block_idx < end_block_idx; block_idx += NUM_WARPS) {
const int64_t physical_block_number = static_cast<int64_t>(block_table[block_idx]);
for (int i = 0; i < NUM_TOKENS_PER_THREAD_GROUP; i++) {
const int physical_block_offset = (thread_group_idx + i * WARP_SIZE) % BLOCK_SIZE;
const int token_idx = block_idx * BLOCK_SIZE + physical_block_offset;
K_vec k_vecs[NUM_VECS_PER_THREAD];
for (int j = 0; j < NUM_VECS_PER_THREAD; j++) {
const scalar_t* k_ptr = k_cache + physical_block_number * kv_block_stride
+ kv_head_idx * kv_head_stride
+ physical_block_offset * x;
const int vec_idx = thread_group_offset + j * THREAD_GROUP_SIZE;
const int offset1 = (vec_idx * VEC_SIZE) / x;
const int offset2 = (vec_idx * VEC_SIZE) % x;
k_vecs[j] = *reinterpret_cast<const K_vec*>(k_ptr + offset1 * BLOCK_SIZE * x + offset2);
}
float qk = scale * Qk_dot<scalar_t, THREAD_GROUP_SIZE>::dot(q_vecs[thread_group_offset], k_vecs);
qk += (alibi_slope != 0) ? alibi_slope * (token_idx - context_len + 1) : 0;
if (thread_group_offset == 0) {
const bool mask = token_idx >= context_len;
logits[token_idx - start_token_idx] = mask ? 0.f : qk;
qk_max = mask ? qk_max : fmaxf(qk_max, qk);
}
}
}
|
计算 softmax
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
for (int mask = WARP_SIZE / 2; mask >= THREAD_GROUP_SIZE; mask /= 2) {
qk_max = fmaxf(qk_max, __shfl_xor_sync(uint32_t(-1), qk_max, mask));
}
if (lane == 0) {
red_smem[warp_idx] = qk_max;
}
qk_max = lane < NUM_WARPS ? red_smem[lane] : -FLT_MAX;
for (int mask = NUM_WARPS / 2; mask >= 1; mask /= 2) {
qk_max = fmaxf(qk_max, __shfl_xor_sync(uint32_t(-1), qk_max, mask));
}
qk_max = __shfl_sync(uint32_t(-1), qk_max, 0);
float exp_sum = 0.f;
for (int i = thread_idx; i < num_tokens; i += NUM_THREADS) {
float val = __expf(logits[i] - qk_max);
logits[i] = val;
exp_sum += val;
}
exp_sum = block_sum<NUM_WARPS>(&red_smem[NUM_WARPS], exp_sum);
const float inv_sum = __fdividef(1.f, exp_sum + 1e-6f);
for (int i = thread_idx; i < num_tokens; i += NUM_THREADS) {
logits[i] *= inv_sum;
}
|
取 v 和第二个矩阵乘法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
|
constexpr int V_VEC_SIZE = MIN(16 / sizeof(scalar_t), BLOCK_SIZE);
using V_vec = typename Vec<scalar_t, V_VEC_SIZE>::Type;
using L_vec = typename Vec<scalar_t, V_VEC_SIZE>::Type;
using Float_L_vec = typename FloatVec<L_vec>::Type;
constexpr int NUM_V_VECS_PER_ROW = BLOCK_SIZE / V_VEC_SIZE;
constexpr int NUM_ROWS_PER_ITER = WARP_SIZE / NUM_V_VECS_PER_ROW;
constexpr int NUM_ROWS_PER_THREAD = DIVIDE_ROUND_UP(HEAD_SIZE, NUM_ROWS_PER_ITER);
float accs[NUM_ROWS_PER_THREAD];
for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
accs[i] = 0.f;
}
scalar_t zero_value;
zero(zero_value);
for (int block_idx = start_block_idx + warp_idx; block_idx < end_block_idx; block_idx += NUM_WARPS) {
const int64_t physical_block_number = static_cast<int64_t>(block_table[block_idx]);
const int physical_block_offset = (lane % NUM_V_VECS_PER_ROW) * V_VEC_SIZE;
const int token_idx = block_idx * BLOCK_SIZE + physical_block_offset;
L_vec logits_vec;
from_float(logits_vec, *reinterpret_cast<Float_L_vec*>(logits + token_idx - start_token_idx));
const scalar_t* v_ptr = v_cache + physical_block_number * kv_block_stride
+ kv_head_idx * kv_head_stride;
for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
const int row_idx = lane / NUM_V_VECS_PER_ROW + i * NUM_ROWS_PER_ITER;
if (row_idx < HEAD_SIZE) {
const int offset = row_idx * BLOCK_SIZE + physical_block_offset;
V_vec v_vec = *reinterpret_cast<const V_vec*>(v_ptr + offset);
if (block_idx == num_context_blocks - 1) {
scalar_t* v_vec_ptr = reinterpret_cast<scalar_t*>(&v_vec);
for (int j = 0; j < V_VEC_SIZE; j++) {
v_vec_ptr[j] = token_idx + j < context_len ? v_vec_ptr[j] : zero_value;
}
}
accs[i] += dot(logits_vec, v_vec);
}
}
}
for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
float acc = accs[i];
for (int mask = NUM_V_VECS_PER_ROW / 2; mask >= 1; mask /= 2) {
acc += __shfl_xor_sync(uint32_t(-1), acc, mask);
}
accs[i] = acc;
}
... # 中间一些处理逻辑
#pragma unroll
for (int i = 0; i < NUM_ROWS_PER_THREAD; i++) {
const int row_idx = lane / NUM_V_VECS_PER_ROW + i * NUM_ROWS_PER_ITER;
if (row_idx < HEAD_SIZE && lane % NUM_V_VECS_PER_ROW == 0) {
from_float(*(out_ptr + row_idx), accs[i]);
}
}
}
|
Next Step
对于目前的 LLM 来说，一种广泛应用的场景会固定若干个 System
Message，相当于 Prompt 是重复的。但每次生成，都需要重新计算每个 System
Message 的 kv cache。因此，这一步是可以优化的。vLLM
在论文中提到了这一点，但目前 vLLM 尚未实现。
System Message 预生成 kv
cache
可以先给定若干 System Message，计算好 kv
cache，以字典的形式存储。在请求时，带上标识符，在字典中找到对应的 kv
cache，在生成时直接拼上，而不计算这一部分的 kv cache。
策略赋值更新 kv cache
以工具调用为例，可以预先生成工具调用结果的所有 token 的 kv
cache，加速生成。
- 在实现 multi token attention 的基础上
- 调度处理
对于这两种都依赖于 multi token attention，而这一个 vLLM 是直接调用
xformers 的 xops.memory_efficient_attention_forward
实现的。这种方式当前只能在第一次生成时使用，没法拼接？
- 比如总共 10 个 prompt token，现在一次性生成 10 个 token 的 kv
cache。期望分两次各生成前 5 个和后 5 个的 token，将 kv cache
拼起来，得到的结果不一致
相关文章：Post not found: PyTorch/pytorch_cpp_extension.md
xops.memory_efficient_attention_forward 学习